
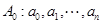
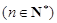 ,满足
,满足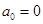 ,
,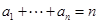 .若存在最小的正整数
.若存在最小的正整数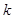 ,使得
,使得 ,则可定义变换
,则可定义变换 ,变换
,变换 将数列
将数列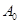 变为数列
变为数列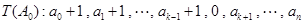 .设
.设 ,
,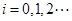 .
.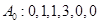 ,试写出数列
,试写出数列 ;若数列
;若数列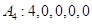 ,试写出数列
,试写出数列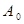 ;
;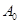 ,经过有限次
,经过有限次 变换,可将数列
变换,可将数列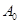 变为数列
变为数列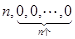 ;
;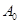 ,经过有限次
,经过有限次 变换,可变为数列
变换,可变为数列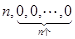 .设
.设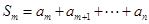 ,
,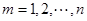 ,求证
,求证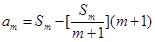 ,其中
,其中 表示不超过
表示不超过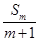 的最大整数.
的最大整数.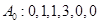 ,则
,则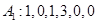 ;
;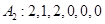 ;
; 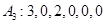 ;
;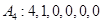 ;
; 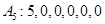 .
.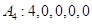 ,则
,则 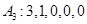 ;
; 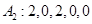 ;
; 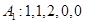 ;
; 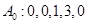 . ………4分
. ………4分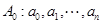 满足
满足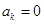 及
及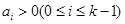 ,则定义变换
,则定义变换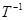 ,变换
,变换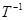 将数列
将数列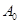 变为数列
变为数列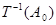 :
: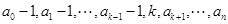 .
.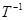 和
和 是互逆变换. ………5分
是互逆变换. ………5分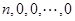 连续实施变换
连续实施变换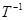 (一直不能再作
(一直不能再作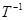 变换为止)得
变换为止)得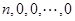
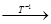
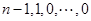
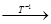
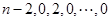
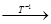

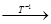
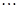
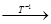
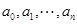 ,
,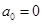 (若
(若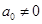 ,则还可作变换
,则还可作变换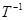 ).反过来对
).反过来对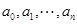 作有限次变换
作有限次变换 ,即可还原为数列
,即可还原为数列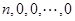 ,因此存在数列
,因此存在数列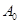 满足条件.
满足条件.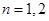 是显然的,假设唯一性对
是显然的,假设唯一性对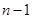 成立,考虑
成立,考虑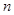 的情形.
的情形.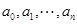 及
及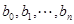 均可经过有限次
均可经过有限次 变换,变为
变换,变为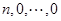 ,这里
,这里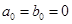 ,
,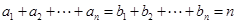
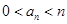 ,则由变换
,则由变换 的定义,不能变为
的定义,不能变为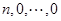 ;
;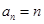 ,则
,则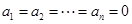 ,经过一次
,经过一次 变换,有
变换,有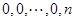
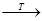
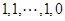
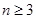 ,可知
,可知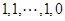 (至少3个1)不可能变为
(至少3个1)不可能变为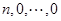 .
.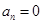 ,同理
,同理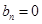 令
令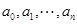
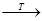
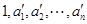 ,
,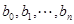
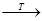
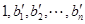 ,
,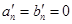 ,所以
,所以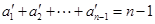 ,
,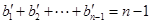 .
.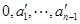
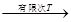
 ,
,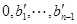
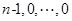 ,
,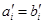 ,
,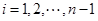 .
. 与
与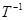 互逆,有
互逆,有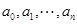
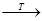
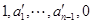 ,
,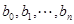
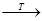
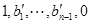 ,
,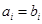 ,
,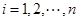 ,从而唯一性得证. ………9分
,从而唯一性得证. ………9分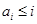
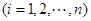 ,这是由于若对某个
,这是由于若对某个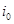 ,
,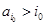 ,则由变换的定义可知,
,则由变换的定义可知,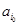 通过变换,不能变为
通过变换,不能变为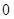 .由变换
.由变换 的定义可知数列
的定义可知数列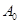 每经过一次变换,
每经过一次变换,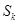 的值或者不变,或者减少
的值或者不变,或者减少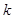 ,由于数列
,由于数列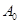 经有限次变换
经有限次变换 ,变为数列
,变为数列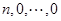 时,有
时,有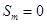 ,
,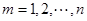 ,
,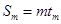
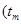 为整数
为整数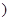 ,于是
,于是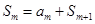
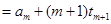 ,
,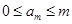 ,
,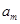 为
为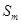 除以
除以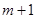 后所得的余数,即
后所得的余数,即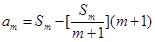 .………13分
.………13分

科目:高中数学 来源:不详 题型:解答题
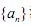 满足:
满足: ,且
,且

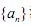 的前n项和为S n,问:是否存在正整数m、n,使得
的前n项和为S n,问:是否存在正整数m、n,使得
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
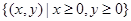 内植树,第一棵树在
内植树,第一棵树在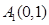 点,第二棵树在
点,第二棵树在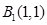 点,第三棵树在C1(1,0)点,第四棵树
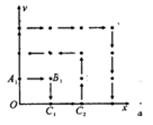
点,第三棵树在C1(1,0)点,第四棵树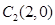 点,接着按图中箭头方向每隔一个单位种一棵树,那么第2011棵树所在的点的坐标是( )
点,接着按图中箭头方向每隔一个单位种一棵树,那么第2011棵树所在的点的坐标是( )| A.(13,44) | B.(12,44) | C.(13,43) | D.(14,43) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (n≥2,n∈N*).
(n≥2,n∈N*).
 与
与 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com