
椭圆 过点
过点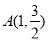 ,离心率为
,离心率为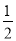 ,左、右焦点分别为
,左、右焦点分别为 ,过
,过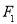 的直线交椭圆于
的直线交椭圆于 两点.
两点.
(1)求椭圆C的方程;
(2)当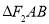 的面积为
的面积为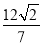 时,求直线的方程.
时,求直线的方程.
(1) ;(2)直线方程为:
;(2)直线方程为: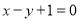 或
或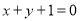 .
.
【解析】
试题分析:本题主要考查椭圆的标准方程及其几何性质、直线的标准方程、直线与椭圆相交问题、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由于椭圆过点A,将A点坐标代入得到a和b的关系式,再利用椭圆的离心率得到a与c的关系式,从而求出a和b,得到椭圆的标准方程;第二问,过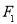 的直线有特殊情况,即当直线的倾斜角为
的直线有特殊情况,即当直线的倾斜角为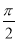 时,先讨论,再讨论斜率不不为
时,先讨论,再讨论斜率不不为 的情况,将直线方程与椭圆方程联立,利用韦达定理得到
的情况,将直线方程与椭圆方程联立,利用韦达定理得到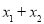 和
和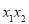 ,代入到三角形面积公式中,解出k的值,从而得到直线方程.
,代入到三角形面积公式中,解出k的值,从而得到直线方程.
试题解析:(1)因为椭圆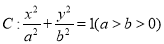 过点
过点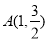 ,所以
,所以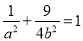 ①,又因为离心率为
①,又因为离心率为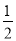 ,所以
,所以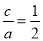 ,所以
,所以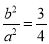 ②,解①②得
②,解①②得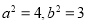 .
.
所以椭圆的方程为: (4分)
(4分)
(2)①当直线的倾斜角为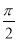 时,
时,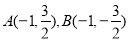 ,
,
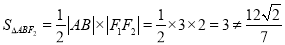 ,不适合题意。 (6分)
,不适合题意。 (6分)
②当直线的倾斜角不为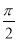 时,设直线方程
时,设直线方程 ,
,
代入 得:
得: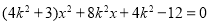 (7分)
(7分)
设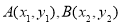 ,则
,则 ,
,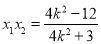 ,
,
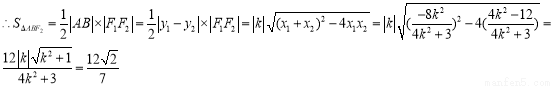
 ,
,
所以直线方程为: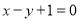 或
或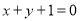 (12分)
(12分)
考点:椭圆的标准方程及其几何性质、直线的标准方程、直线与椭圆相交问题、三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届浙江富阳二中高二下学期第三次质量检测理科数学试卷(解析版) 题型:解答题
已知 是椭圆
是椭圆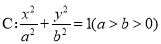 的左,右顶点,
的左,右顶点, ,过椭圆C的右焦点
,过椭圆C的右焦点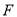 的直线交椭圆于点
的直线交椭圆于点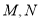 ,交直线
,交直线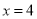 于点
于点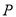 ,且直线
,且直线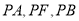 的斜率成等差数列,
的斜率成等差数列,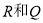 是椭圆上的两动点,
是椭圆上的两动点,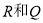 的横坐标之和为2,
的横坐标之和为2, 的中垂线交
的中垂线交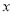 轴于
轴于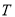 点
点
(1)求椭圆 的方程;(2)求△
的方程;(2)求△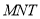 的面积的最大值
的面积的最大值

查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试理科数学试卷(解析版) 题型:选择题
执行如图中的程序框图,若输出的结果为21,则判断框中应填( )
(A)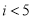 (B)
(B)  (C)
(C)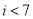 (D)
(D)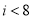
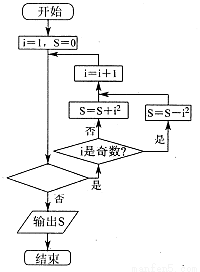
查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:填空题
设O是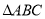 的三边中垂线的交点,
的三边中垂线的交点,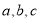 分别为角
分别为角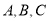 对应的边,已知
对应的边,已知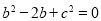 ,则
,则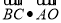 的范围是___________.
的范围是___________.
查看答案和解析>>
科目:高中数学 来源:2015届河南省顶级名校高三入学定位考试文科数学试卷(解析版) 题型:选择题
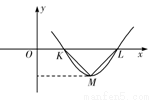
设偶函数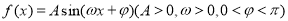 的部分图象如图所示,
的部分图象如图所示,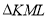 为等腰直角三角形,
为等腰直角三角形,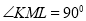 ,
,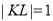 ,则
,则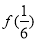 的值为( )
的值为( )
(A)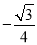 (B)
(B)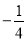 (C)
(C)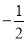 (D)
(D)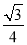
查看答案和解析>>
科目:高中数学 来源:2015届河南省开封市高三上学期定位模拟考试文科数学试卷(解析版) 题型:选择题
对一个容量为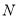 的总体抽取容量为
的总体抽取容量为 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为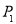 、
、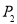 、
、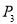 ,则( )
,则( )
A. B.
B.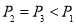 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com