
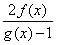 +f(x)为
+f(x)为科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
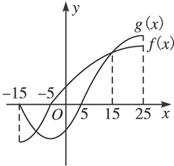
A.[5,25] B.(-5,25]
C.(5,25]∪(-15,-5) D.(-15,5]∪[15,25]
查看答案和解析>>
科目:高中数学 来源: 题型:
已知二次函数y=f(x)在x=![]() 处取得最小值-
处取得最小值-![]() (t>0),f(1)=0.
(t>0),f(1)=0.
(1)求y=f(x)的表达式;
(2)若任意实数x都满足等式f(x)·g(x)+anx+bn=xn+1[g(x)]为多项式,n∈N*),试用t表示an和bn;
(3)设圆Cn的方程为(x-an)2+(y-bn)2=rn2,圆Cn与Cn+1外切(n=1,2,3,…);{rn}是各项都是正数的等比数列,记Sn为前n个圆的面积之和,求rn、Sn.
查看答案和解析>>
科目:高中数学 来源:2010年江西省高三上学期开学模拟考试文科数学卷 题型:解答题
设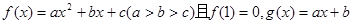
(1)求证:函数y=f(x)与y=g(x)的图像有两个交点;
(2)设f(x)与g(x)的图像交点A、B在x轴上的射影为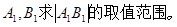
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com