
已知抛物线C:x2=4y的焦点为F,过点K(0,-1)的直线l与C相交于A,B两点,点A关于y轴的对称点为D.
(1)证明:点F在直线BD上;
(2)设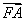 ·
·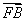 =
=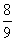 ,求∠DBK的平分线与y轴的交点坐标.
,求∠DBK的平分线与y轴的交点坐标.
解:(1)证明:设A(x1,y1),B(x2,y2),
D(-x1,y1),l的方程为y=kx-1,
由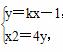 得x2-4kx+4=0,
得x2-4kx+4=0,
从而x1+x2=4k,x1x2=4.
直线BD的方程为y-y1=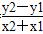 (x+x1),
(x+x1),
即y-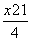 =
=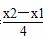 (x+x1),
(x+x1),
令x=0,得y=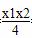 =1,所以点F在直线BD上.
=1,所以点F在直线BD上.
(2)因为FA―→·FB―→=(x1,y1-1)·(x2,y2-1)=x1x2+(y1-1)·(y2-1)=8-4k2,
故8-4k2=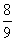 ,解得k=±
,解得k=±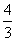 ,
,
所以l的方程为4x-3y-3=0,4x+3y+3=0.
又由(1)得x2-x1=±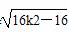 =±
=±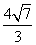 ,
,
故直线BD的斜率为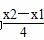 =±
=±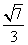 ,
,
因而直线BD的方程为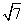 x-3y+3=0,
x-3y+3=0,
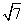 x+3y-3=0.
x+3y-3=0.
设∠DBK的平分线与y轴的交点为M(0,t),
则M(0,t)到l及BD的距离分别为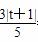 ,
,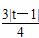 ,
,
由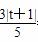 =
=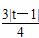 ,得t=
,得t=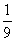 或t=9(舍去),
或t=9(舍去),
所以∠DBK的平分线与y轴的交点为
M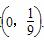 .
.


科目:高中数学 来源: 题型:
某校校运会期间,来自甲、乙两个班级共计6名学生志愿者随机平均分配到后勤组、保洁组、检录组,并且后勤组至少有一名甲班志愿者的概率为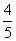 .
.
(1)求6名志愿者中来自甲、乙两个班级的学生各有几人;
(2)设在后勤组的甲班志愿者人数为X,求随机变量X的概率分布及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
某企业为了更好地了解设备改造与生产合格品的关系,随机抽取了180件产品进行分析,其中设备改造前生产的合格品有36件,不合格品有49件,设备改造后生产的合格品有65件,不合格品有30件,根据这些数据,能得出什么结论?
查看答案和解析>>
科目:高中数学 来源: 题型:
把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列{an},若an=911,则n=

查看答案和解析>>
科目:高中数学 来源: 题型:
已知公比不为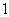 的等比数列
的等比数列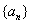 的首项
的首项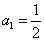 ,前
,前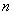 项和为
项和为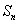 ,且
,且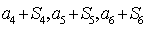 成等差数列.
成等差数列.
(1)求等比数列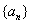 的通项公式;
的通项公式;
(2)对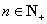 ,在
,在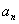 与
与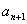 之间插入
之间插入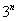 个数,使这
个数,使这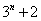 个数成等差数列,记插入的这
个数成等差数列,记插入的这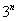 个数的和为
个数的和为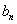 ,求数列
,求数列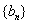 的前
的前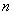 项和
项和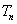 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com