
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据
![]()
(1)利用所给数据求年需求量与年份之间的回归直线方程![]() ;
;
(2)利用(1)计算2002年和2006年粮食需求量的残差;
(3)利用(1)中所求出的直线方程预测该地2012年的粮食需求量。
公式:
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域和值域均为[-a,a]的函数y=![]() 和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
和y=g(x)的图象如图所示,其中a>c>b>0,给出下列四个结论正确结论的是( )
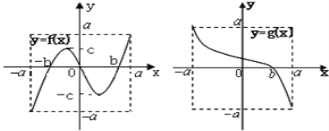
A.方程f[g(x)]=0有且仅有三个解B.方程g[f(x)]=0有且仅有三个解
C.方程f[f(x)]=0有且仅有九个解D.方程g[g(x)]=0有且仅有一个解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某周末,郑州方特梦幻王国汇聚了八方来客. 面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同. 某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查. 调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.

(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
(2)根据列联表的数据,判断是否有99%的把握认为选择哪个主题公园与年龄有关.
附参考公式与表:![]() .
.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com