Question

【题目】计算题
（1）已知集合A={x|3＜x＜7}，B={x|2＜x＜10}，求A∪B，A∩B，RA
（2）计算下列各式 ①
②（2a b ）（﹣6a b ）÷（﹣3a b ）

Answer 1

【答案】
（1）解：∵A={x|3＜x＜7}，B={x|2＜x＜10}，

∴A∪B={x|2＜x＜10}，A∩B={x|3＜x＜7}，RA={x|x≤3或x≥7}

（2）解：① = = =6，

② 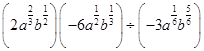= =4ab0=4a

【解析】（1）根据集合的交并补的定义计算即可，（2）①根据对数的运算性质计算即可，②根据幂的运算性质计算即可．
【考点精析】利用交、并、补集的混合运算对题目进行判断即可得到答案，需要熟知求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法．