
分析 把a分离出来,然后用导数,判断单调性从而求出最值.
解答 解:∵$\frac{cosx-1}{{x}^{2}}>a$在$(0,\frac{π}{2})$恒成立
∴$f(x)=\frac{cosx-1}{{x}^{2}}$$;{f}^{′}(x)=\frac{-[xsinx+2(1-cosx)]}{{x}^{3}}$;
∵xsinx>0,1-cosx>0
∴f′(x)<0,f(x)在(0,$\frac{π}{2}$)上单调递减.
$f(x)_{min}=f(\frac{π}{2})=-\frac{4}{{π}^{2}}$
即有a$≤-\frac{4}{{π}^{2}}$.
故答案为:a$≤-\frac{4}{{π}^{2}}$.
点评 本题主要考察了导数的综合应用,考察了转化思想,属于中档题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:解答题
已知圆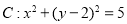 ,直线
,直线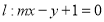 .
.
(1)求证:对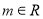 ,直线
,直线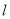 与圆
与圆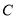 总有两个不同交点;
总有两个不同交点;
(2)若圆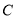 与直线
与直线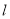 相交于
相交于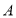 ,
,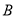 两点,求弦
两点,求弦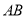 的长度最小值.
的长度最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
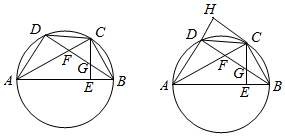 如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
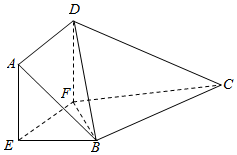 在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,
在直角梯形ABCD中,AB∥DC,AD⊥AB,DC=3,AB=2,AD=1,AE=EB,DF=1,现把它沿FE折起,得到如图所示几何体,连接DB,AB,DC,使DC=$\sqrt{5}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com