
 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
已知圆 ,从点
,从点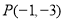 发出的光线,经
发出的光线,经 轴反射后恰好经过圆心
轴反射后恰好经过圆心 ,则入射光线的斜率为( )
,则入射光线的斜率为( )
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
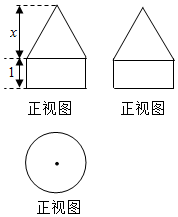 如图,是一个几何体的三视图,其中正视图与侧视图完全相同,均为等边三角形与矩形的组合,俯视图为圆,若已知该几何体的表面积为16π,则x=$2\sqrt{3}$.
如图,是一个几何体的三视图,其中正视图与侧视图完全相同,均为等边三角形与矩形的组合,俯视图为圆,若已知该几何体的表面积为16π,则x=$2\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
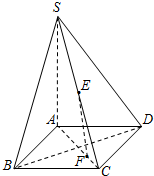 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,E为SC的中点,F为AC上一点,且AB=2,SA=2$\sqrt{2}$.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,E为SC的中点,F为AC上一点,且AB=2,SA=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°
在四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且AB=AA1,∠A1AB=∠A1AD=60°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
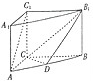 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AB=5,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=AA1=4,AB=5,D是线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com