
(1)求C;
(2)已知c=![]() ,△ABC的面积为S=
,△ABC的面积为S=![]() ,求a+b.
,求a+b.
思路解析:此题主要考查向量的数量积与解三角形的知识,使解三角形不再孤立,也体现了向量的工具性作用.(1)已知两向量的夹角,运用数量积来求C.(2)已知面积,利用面积公式求出a与b的积,再利用余弦定理来求a2+b2,进而求出a+b.
解:(1)∵m=(cos![]() ,sin
,sin![]() ),n=(cos
),n=(cos![]() ,-sin
,-sin![]() ),
),
∴m·n=cos2![]() -sin2
-sin2![]() =cosC.
=cosC.
又m·n=|m|·|n|cos![]() =1×1×
=1×1×![]() =
=![]() ,
,
∴cosC=![]() .∴C=
.∴C=![]() .
.
(2)∵c2=a2+b2-2abcosC,c=![]() ,
,
∴![]() =a2+b2-ab=(a+b)2-3ab.
=a2+b2-ab=(a+b)2-3ab.
∵S△ABC=![]() absinC=
absinC=![]() absin
absin![]() =
=![]() ab=
ab=![]() ,
,
∴ab=6.
从而(a+b)2=![]() +3ab=
+3ab=![]() +18=
+18=![]() ,∴a+b=
,∴a+b=![]() .
.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源:2012-2013学年吉林省实验中学高一上学期期末考试数学试卷(带解析) 题型:填空题
在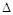 ABC中,M是BC的中点,AM ="3,BC" =10,则
ABC中,M是BC的中点,AM ="3,BC" =10,则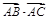 =______________
=______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com