
(Ⅰ)求动圆圆心的轨迹C的方程;
(Ⅱ)若直线l被轨迹C所截得的线段的中点坐标为(-20,-16),求直线l的方程;
(Ⅲ)若点P在直线l上,且过点P的椭圆E以轨迹,C的焦点为焦点,试求点P在什么位置时,椭圆E的长轴最短,并求出这个具有最短长轴的椭圆E的方程.
解:(Ⅰ)设动圆半径为r,圆心为M,则由已知得:
 ∴|MF2|-|MF1|=2
∴|MF2|-|MF1|=2![]() .
.
∴动圆圆心的轨迹C为以F1,F2为焦点,实轴长为2![]() 的双曲线的左支,易得其方程为:
的双曲线的左支,易得其方程为:![]() =1(x<0).
=1(x<0).
(Ⅱ)设l的方程为:y+16=A(x+20),并设l与轨迹C的交点坐标为(x1,y1),(x2,y2),则由已知得:
![]() =-20,即x1+x2=-40 ①
=-20,即x1+x2=-40 ①
由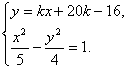 消去y得:
消去y得:
(4-5k2)x2-10k(20k-16)x-5(20k-16)2-20=0,
∴x1+x2=![]() ②
②
由①②得:![]() =-40,∴k=1.
=-40,∴k=1.
∴所求直线l的方程为y=x+4;
(Ⅲ)椭圆的长轴K等于|PF1|+|PF2|,要长轴最短,只需在直线l上找一点P,使点P到F1、F2的距离之和最小.由平面几何知识知:作F1关于l的对称点Q,连接QF2交直线l于点P,则点P即为所求点,坐标为(![]() ).
).
此时长轴2a=|PF1|+|PF2|=|PQ|+|PF2|=|QF2|=5![]() .
.
从而a2=![]() ,c=3.∴b2=a2-c2=
,c=3.∴b2=a2-c2=![]() -9=
-9=![]() .
.
∴椭圆E的方程为: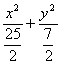 =1.
=1.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
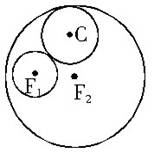
如图所示,已知动圆C与半径为2的圆F1外切,与半径为8的圆F2内切,且F1F2=6,
(1)求证:动圆圆心C的轨迹是椭圆;
(2)建立适当直角坐标系,求出该椭圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com