已知动圆过定点F1(-3,0),且与圆O:(x-3)2+y2=100相内切,
(1)求动圆的圆心的轨迹曲线C.
(2)若P是C上的一点,F2为圆O的圆心且∠F1PF2=60°,求△F1PF2的面积.
【答案】
分析:(1)设切点为N,动圆与圆O内切,则F
2,M,N三点共线,且|MF
1|=|MN|,所以M到定点F
1,F
2的距离之和为定值10>|F
1F
2|=6,由此能求出M的轨迹方程.
(2)设|PF
1|=r
1,|PF
2|=r
2,则r
1+r
2=2a=10⇒r
12+2r
1r
2+r
2=100.在△PF
1F
2中,由勾股定理得r
12+r
23-r
1r
2=4c
2=36,由此能求出△F
1PF
2的面积.
解答:解:(1)设切点为N,动圆与圆O内切,
则F
2,M,N三点共线,且|MF
1|=|MN|
∴|MF
1|+|MF
2|=|MF
1|+|MF
2|=|NF
2|
即M到定点F
1,F
2的距离之和为定值10>|F
1F
2|=6
故M的轨迹是以F
1,F
2为焦点的椭圆
易知c=3,a=5,b=4
M的轨迹方程是

.
(2)设|PF
1|=r
1,|PF
2|=r
2,
则r
1+r
2=2a=10⇒r
12+2r
1r
2+r
2=100(1)
又在△PF
1F
2中,由勾股定理得r
12+r
22-r
1r
2=4c
2=36(2)
(1)-(2)得
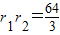
∴
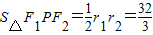 点评:
点评:本题考查点的轨迹的求法和计算△F
1PF
2的面积.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

 .
.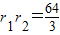
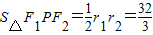


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案