
错解:∵x+y=(x+y)![]() ·
·![]() ,∴(x+y)min=
,∴(x+y)min=![]() .
.
错因分析:x+y≥![]() 中等号成立的条件是x=y,
中等号成立的条件是x=y,![]() ≥
≥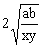 中等号成立的条件是
中等号成立的条件是![]() ,而
,而![]() =1,∴x=2a,y=2b.此时a不一定等于b,故上述解法有误.
=1,∴x=2a,y=2b.此时a不一定等于b,故上述解法有误.
正解一:(消元法)∵![]() =1,∴y=
=1,∴y=![]() 且x>a.
且x>a.
∴x+y=x+![]() =x+
=x+![]() =x+b+
=x+b+![]() =x-a+
=x-a+![]() +a+b≥
+a+b≥![]() +a+b=(
+a+b=(![]() +
+![]() )2.
)2.
正解二:(妙用“1”)x+y=(x+y)(![]() )=a+
)=a+![]() +b≥a+b+
+b≥a+b+![]() =(
=(![]() +
+![]() )2.
)2.
正解三:(三角代换)令![]() =cos2θ,
=cos2θ,![]() =sin2θ,则x+y=asec2θ+bcsc2θ=a(1+tan2θ)+b(1+cot2θ)
=sin2θ,则x+y=asec2θ+bcsc2θ=a(1+tan2θ)+b(1+cot2θ)
=a+b+atan2θ+bcot2θ≥a+b+![]() =(
=(![]() )2.
)2.
上述三种解法均可得出当且仅当x=![]() +a,y=
+a,y=![]() +b时取等号,故(x+y)min=(
+b时取等号,故(x+y)min=(![]() )2.
)2.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com