
分析 根据三角函数同角的关系式,求出tanα,然后利用两角和差的正切公式进行求解即可.
解答 解:∵α∈(-$\frac{π}{2}$,0),cosα=$\frac{\sqrt{5}}{5}$,
∴sinα=-$\sqrt{1-(\frac{\sqrt{5}}{5})^{2}}$=-$\sqrt{1-\frac{5}{25}}=-\sqrt{\frac{20}{25}}$=-$\frac{2\sqrt{5}}{5}$,
则tanα=$\frac{sinα}{cosα}$=$\frac{-\frac{2\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}}$=-2,
则tan(α-$\frac{π}{4}$)=$\frac{tanα-tan\frac{π}{4}}{1+tanαtan\frac{π}{4}}$=$\frac{-2-1}{1-2}=\frac{-3}{-1}=3$,
故答案为:3.
点评 本题主要考查三角函数值的求解,利用三角函数的同角关系式以及两角和差的正切公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
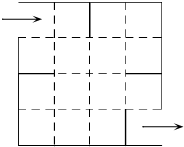 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |MF|>d | B. | |MF|<d | C. | |MF|=d | D. | 与a,b的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com