Question

（2013•广州一模）如图，在三棱柱ABC-A₁B₁C₁中，△ABC是边长为2的等边三角形，AA₁⊥平面ABC，D，E分别是CC₁，AB的中点．
（1）求证：CE∥平面A₁BD；
（2）若H为A₁B上的动点，当CH与平面A₁AB所成最大角的正切值为

15

2

时，求平面A₁BD与平面ABC所成二面角（锐角）的余弦值．

Answer 1

分析：（1）通过补形，延长延长A₁D交AC的延长线于点F，连接BF，从而可证明CE∥BF，然后由线面平行的判定定理得证；
（2）由已知找出C点在平面A₁AB上的射影CE，CE为定值，要使直线CH与平面A₁AB所成最大角的正切值为

15

2

，则点H到E点的距离应最小，由此得到H的位置，进一步求出EH的长度，则在直角三角EHB中可得到BH的长度，利用已知条件证出BF⊥平面A₁AB，从而得到∠EBH为平面A₁BD与平面ABC所成的二面角，在直角三角形EHB中求其余弦值．
本题也可以A为坐标原点，建立空间直角坐标系，利用空间向量解决．

解答：法一、
（1）证明：如图，

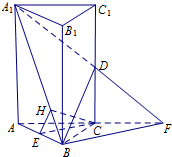
延长A₁D交AC的延长线于点F，连接BF．
∵CD∥AA₁，且CD=

1

2

AA₁，
∴C为AF的中点．
∵E为AB的中点，
∴CE∥BF．
∵BF?平面A₁BD，CE?平面A₁BD，
∴CE∥平面A₁BD．
（2）解：∵AA₁⊥平面ABC，CE?平面ABC，
∴AA₁⊥CE．
∵△ABC是边长为2的等边三角形，E是AB的中点，
∴CE⊥AB，CE=

3

2

AB=

3

．
∵AB?平面A₁AB，AA₁?平面A₁AB，AB∩AA₁=A，
∴CE⊥平面A₁AB．
∴∠EHC为CH与平面A₁AB所成的角．
∵CE=

3

，
在Rt△CEH中，tan∠EHC=

CE

EH

=

3

EH

，
∴当EH最短时，tan∠EHC的值最大，则∠EHC最大．
∴当EH⊥A₁B时，∠EHC最大．此时，tan∠EHC=

CE

EH

=

3

EH

=

15

2

．
∴EH=

2 5

5

．
∵CE∥BF，CE⊥平面A₁AB，
∴BF⊥平面A₁AB．
∵AB?平面A₁AB，A₁B?平面A₁AB，
∴BF⊥AB，BF⊥A₁B．
∴∠ABA₁为平面A₁BD与平面ABC所成二面角（锐角）．
在Rt△EHB中，BH=

EB2-EH2

=

5

5

，cos∠ABA₁=

BH

EB

=

5

5

．
∴平面A₁BD与平面ABC所成二面角（锐角）的余弦值为

5

5

．
法二、
（1）证明：如图，

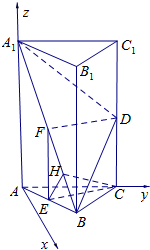
取A₁B的中点F，连接DF、EF．
∵E为AB的中点，
∴EF∥AA₁，且EF=

1

2

AA1．
∵CD∥AA₁，且CD=

1

2

AA₁，
∴EF∥CD，EF=CD．
∴四边形EFDC是平行四边形．
∴CE∥DF．
∵DF?平面A₁BD，CE?平面A₁BD，
∴CE∥平面A₁BD．
（2）解：∵AA₁⊥平面ABC，CE?平面ABC，
∴AA₁⊥CE．
∵△ABC是边长为2的等边三角形，E是AB的中点，
∴CE⊥AB，CE=

3

2

AB=

3

．
∵AB?平面A₁AB，AA₁?平面A₁AB，AB∩AA₁=A，
∴CE⊥平面A₁AB．
∴∠EHC为CH与平面A₁AB所成的角．
∵CE=

3

，
在Rt△CEH中，tan∠EHC=

CE

EH

=

3

EH

，
∴当EH最短时，tan∠EHC的值最大，则∠EHC最大．
∴当EH⊥A₁B时，∠EHC最大．此时，tan∠EHC=

CE

EH

=

3

EH

=

15

2

．
∴EH=

2 5

5

．
在Rt△EHB中，BH=

EB2-EH2

=

5

5

．
∵Rt△EHB～Rt△A₁AB，
∴

EH

AA1

=

BH

AB

，即

2 5 5

AA1

=

5 5

2

．
∴AA₁=4．
以A为原点，与AC垂直的直线为x轴，AC所在的直线为y轴，AA₁所在的直线为z轴，
建立空间直角坐标系A-xyz．
则A（0，0，0），A₁（0，0，4），B(

3

，1，0)，D（0，2，2）．
∴

AA1

=（0，0，4），

A1B

=(

3

，1，-4)，

A1D

=（0，2，-2）．
设平面A₁BD的法向量为n=（x，y，z），
由

n

•

A1B

=0，

n

•

A1D

=0，
得

3 x+y-4z=0 2y-2z=0

，令y=1，则z=1，x=

3

．
∴平面A₁BD的一个法向量为n=(

3

，1，1)．
∵AA₁⊥平面ABC，∴

AA1

=（0，0，4）是平面ABC的一个法向量．
∴cos?n，

AA1

＞=

n• AA1

|n|| AA1 |

=

5

5

．
∴平面A₁BD与平面ABC所成二面角（锐角）的余弦值为

5

5

．

点评：本小题主要考查空间线面位置关系、直线与平面所成的角、二面角等基础知识，考查空间想象、推理论证、抽象概括和运算求解能力，以及化归与转化的数学思想方法．是中档题．