
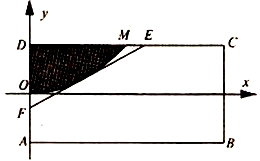
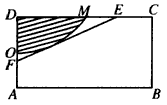
 有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.
有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.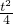
 ,求导,得,y′=
,求导,得,y′=
 ,切线EF的方程为y-m=
,切线EF的方程为y-m= (x-t)
(x-t)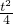 代入,得,y-
代入,得,y-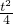 =
= (x-t)
(x-t)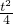 =
= (x-t)中x=0,得,y=-
(x-t)中x=0,得,y=-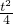

 |DE||DF|=
|DE||DF|= (1+
(1+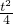 )(
)( )=
)=
 ,当t∈[0,1]时,S′△DEF<0
,当t∈[0,1]时,S′△DEF<0
 ),AF=
),AF=
 时,截去的△DEF的面积最小.
时,截去的△DEF的面积最小.

科目:高中数学 来源: 题型:
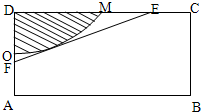 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.
有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,已知AB=4米,AD=2米.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?查看答案和解析>>
科目:高中数学 来源:河北省期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com