练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知对数函数过点，.

    （1）求的解析式，并指出的定义域；

    （2）设，求函数的零点.

    【答案】(1) ，定义域为; (2) 答案见解析

    【解析】

    （1）设函数，带入点可解出a的值，则可得出的解析式.

    再将代入函数f(x)中，由，则可得出的解析式，再根据对数函数的定义可得出的定义域.

    （2）将函数的零点转化为方程的解来求零点，再分类讨论当，，时方程的解.

    解：（1）设函数，∵过点，∴，

    解得,∴.

    ，解不等式组可得的定义域为

    （2）函数的零点是方程的解.

    ，

    因为，所以，所以，即的值域为

    若，则方程无解；

    若，则，所以，方程有且只有一个解；

    若，则，所以，方程有两个解

    综上所述：若，则无零点； 若，则有且只有一个零点；

    若，则有两个零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知

    （1）求函数在的极值.

    （2）证明：在有且仅有一个零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直三棱柱的底面是边长为6的等边三角形，是边上的中点，点满足，平面平面，求：

    (1)侧棱长；

    (2)直线与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）求函数的定义域；

    （2）判断函数的奇偶性，并予以证明；

    （3）求使的的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列，，其前项和满足，其中.

    （1）设，证明：数列是等差数列；

    （2）设，为数列的前项和，求证：；

    （3）设（为非零整数，），试确定的值，使得对任意，都有成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某部门为了解人们对“延迟退休年龄政策”的支持度，随机调查了人，其中男性人.调查发现持不支持态度的有人，其中男性占.分析这个持不支持态度的样本的年龄和性别结构，绘制等高条形图如图所示.

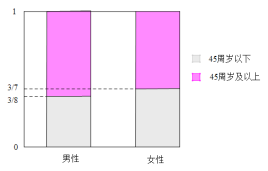
    （1）在持不支持态度的人中，周岁及以上的男女比例是多少？

    （2）调查数据显示，个持支持态度的人中有人年龄在周岁以下.填写下面的列联表，问能否有的把握认为年龄是否在周岁以下与对“延迟退休年龄政策”的态度有关.

    参考公式及数据：，．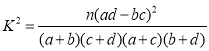

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的左、右焦点分别为，，若椭圆经过点，且的面积为.

    （1）求椭圆的标准方程；

    （2）设斜率为的直线与以原点为圆心，半径为的圆交于，两点，与椭圆交于，两点，且，当取得最小值时，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （Ⅰ）当时，求函数的单调区间；

    （Ⅱ）若曲线在点处的切线与曲线切于点，求的值；

    （Ⅲ）若恒成立，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数有两个零点．

    （1）若函数的两个零点是和，求的值，并写出不等式的解集；

    （2）当时，函数有两个零点和，求的取值范围．

    查看答案和解析>>

    同步练习册答案