
在四棱锥 中,平面
中,平面 平面
平面 ,
, ,在锐角
,在锐角

 中
中 ,并且
,并且 ,
,
(1)点 是
是 上的一点,证明:平面
上的一点,证明:平面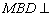 平面
平面 ;
;
(2)若 与平面
与平面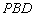 成角
成角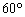 ,当面
,当面 平面
平面 时,
时,
求点 到平面
到平面 的距离.
的距离.
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
在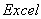 中产生
中产生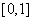 区间上均匀随机数的函数为“
区间上均匀随机数的函数为“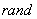 ( )”,在用计算机模拟估计函数
( )”,在用计算机模拟估计函数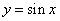 的图像、直线
的图像、直线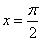 和
和 轴在区间
轴在区间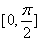 上部分围成的图形面积时,随机点
上部分围成的图形面积时,随机点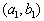 与该区域内的点
与该区域内的点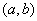 的坐标变换公式为 ( )
的坐标变换公式为 ( )
A. 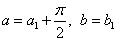 B.
B. 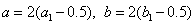
C. 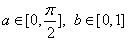 D.
D. 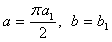
查看答案和解析>>
科目:高中数学 来源: 题型:
在研究打酣与患心脏病之间的关系中,通过收集数据、整理分析数据得“打酣与患心脏病有关”的结论,并且有 以上的把握认为这个结论是成立的。下列说法中正确的是( )
以上的把握认为这个结论是成立的。下列说法中正确的是( )
A.100个心脏病患者中至少有99人打酣
B..1个人患心脏病,那么这个人有99%的概率打酣
C.在100个心脏病患者中一定有打酣的人
D.在100个心脏病患者中可能一个打酣的人都没有
查看答案和解析>>
科目:高中数学 来源: 题型:
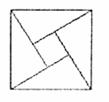
在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为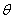 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是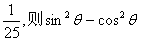 的值等于
的值等于
A.1 B.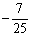 C.
C.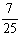 D.
D.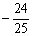
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com