
(1)(2)(3)
【解析】
试题分析:由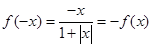 ,所以(1)正确;对于B,不妨设m=
,所以(1)正确;对于B,不妨设m=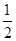 则|f(x)|=
则|f(x)|= 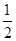 ,即
,即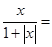
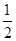 ,得到:x=1或-1,
故B正确;对于C,就是求f(x)单调性,由于f(x)为奇函数,只需讨论在(0,+∞)的单调性即可,当x>0时,f(x)=
,得到:x=1或-1,
故B正确;对于C,就是求f(x)单调性,由于f(x)为奇函数,只需讨论在(0,+∞)的单调性即可,当x>0时,f(x)= 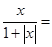
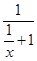 >0,所以在(0,+∞)单调递增且函数值都为正数,所以函数f(x)在(-∞,0)上单调递增且函数值都为负数,又f(0)=0,故f(x)在R上单调递增,所以任意x1,x2
>0,所以在(0,+∞)单调递增且函数值都为正数,所以函数f(x)在(-∞,0)上单调递增且函数值都为负数,又f(0)=0,故f(x)在R上单调递增,所以任意x1,x2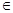 属于R,若x1≠x2,则一定有f(x1)≠f(x2)正确;D错误,令f(x)-kx=
属于R,若x1≠x2,则一定有f(x1)≠f(x2)正确;D错误,令f(x)-kx=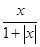 -kx=x(
-kx=x(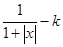 )=0,则有一根为x=0,或
)=0,则有一根为x=0,或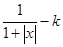 =0,但是
=0,但是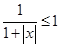 ,而k
,而k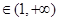 ,所以
,所以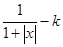 =0恒不成立,所以选择D
=0恒不成立,所以选择D
考点:1.函数的单调性、最值;2.函数的奇偶性、周期性;3.函数零点的判定定理.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2010-2011学年江苏省连云港市东海高级中学高三(上)期中数学试卷(文科)(解析版) 题型:填空题
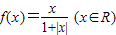 时,则下列结论不正确是 .
时,则下列结论不正确是 .查看答案和解析>>
科目:高中数学 来源:2012年江苏省无锡市辅仁高级中学高三3月联考数学试卷(解析版) 题型:解答题
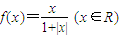 时,则下列结论不正确是 .
时,则下列结论不正确是 .查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市高考数学信息试卷(一)(解析版) 题型:解答题
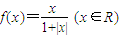 时,则下列结论不正确是 .
时,则下列结论不正确是 .查看答案和解析>>
科目:高中数学 来源:2011年广东省广州大学附属中学高考数学一模试卷(文科)(解析版) 题型:选择题
 时,则下列结论不正确的是( )
时,则下列结论不正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com