
【题目】设集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2﹣1=0},A∩B=B,求实数a的值.
【答案】解:由A={x|x2+4x=0}={0,﹣4},又A∩B=B,∴BA
( 1 )若B=,则x2+2(a+1)x+a2﹣1=0的判别式小于0,即4(a+1)2﹣4(a2﹣1)<0,
∴a<﹣1.
( 2 )若B={0},把x=0代入方程得a=±1
当a=1时,B={﹣4,0}≠{0}.
当a=﹣1时,B={0},∴a=﹣1.
( 3 )若B={﹣4}时,把x=﹣4代入得a=1或a=7.
当a=1时,B={0,﹣4}≠{﹣4},∴a≠1.
当a=7时,B={﹣4,﹣12}≠{﹣4},∴a≠7.
( 4 )若B={0,﹣4},则a=1,当a=1时,B={0,﹣4},∴a=1
综上所述:a≤﹣1或a=1.
【解析】求解一元二次方程化简集合A,根据A∩B=B得到BA,然后分B为空集、单元素集合及双元素集合讨论求解a的值.
【考点精析】本题主要考查了集合的交集运算的相关知识点,需要掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立才能正确解答此题.
B,反之也成立才能正确解答此题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,a2=6,且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列.
(1)求{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 求满足不等式Sn>
}的前n项和为Sn , 求满足不等式Sn> ![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4y﹣4=0,是否存在斜率为1的直线l,使l被圆C截得的弦长AB为直径的圆过原点,若存在求出直线的方程l,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,当x>0时,f(x)=log2( ![]() +a).
+a).
(1)若函数f(x)过点(1,1),求此时函数f(x)的解析式;
(2)若函数g(x)=f(x)+2log2x只有一个零点,求实数a的范围;
(3)设a>0,若对任意实数t∈[ ![]() ,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是奇函数,f(x)=lg(10x+1)+bx是偶函数.
是奇函数,f(x)=lg(10x+1)+bx是偶函数.
(1)求a+b的值.
(2)若对任意的t∈[0,+∞),不等式g(t2﹣2t)+g(2t2﹣k)>0恒成立,求实数k的取值范围.
(3)设 ![]() ,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
,若存在x∈(﹣∞,1],使不等式g(x)>h[lg(10a+9)]成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底数,e=2.71828…).
(e为自然对数的底数,e=2.71828…).
(1)证明:函数f(x)为奇函数;
(2)判断并证明函数f(x)的单调性,再根据结论确定f(m2﹣m+1)+f(﹣ ![]() )与0的大小关系;
)与0的大小关系;
(3)是否存在实数k,使得函数f(x)在定义域[a,b]上的值域为[kea , keb].若存在,求出实数k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,﹣1),
=(m,﹣1), ![]() =(
=( ![]() )
)
(1)若m=﹣ ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)设 ![]() . ①求实数m的值;
. ①求实数m的值;
②若存在非零实数k,t,使得[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ]⊥(﹣k
]⊥(﹣k ![]() +t
+t ![]() ),求
),求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN. 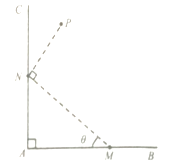
(1)设∠AMN=θ,将工厂与村庄的距离PA表示为θ的函数,记为l(θ),并写出函数l(θ)的定义域;
(2)当θ为何值时,l(θ)有最大值?并求出该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com