
已知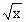 =|cosπt-sinπt|,
=|cosπt-sinπt|,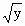 =|cos2πt-sin2πt|,其中-1≤t≤1.
=|cos2πt-sin2πt|,其中-1≤t≤1.
(1)作出函数x=f(t)的图象.
(2)写出y=g(x)的解析式并作出y=g(x)的图象.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:走向清华北大同步导读·高二数学(上) 题型:044
已知椭圆的两焦点 (0,-1)和
(0,-1)和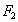 (0,1),直线y=4是该椭圆的一条准线.
(0,1),直线y=4是该椭圆的一条准线.
(1)求椭圆的方程;
(2)已知椭圆上一点P满足 =1,求tan∠
=1,求tan∠ P
P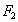 .
.
查看答案和解析>>
科目:高中数学 来源:河南省实验中学2006-2007学年度上学期高三年级期中考试、数学试题(理科) 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:北京市育园中学07届高三数学质量检测数学(理) 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com