
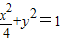 上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是 .
上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是 . 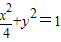 上 里面的自变量x,y可以表示为 x=2cosa y=sina 本题中要求第一象限,这样就应该有0<a<π,设P为(2cosa,sina)这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和,对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa 这样四边形的面积S=S1+S2=sina+cosa也就相当于求解sina+cosa的最大值,0<a<π,sina+cosa=
上 里面的自变量x,y可以表示为 x=2cosa y=sina 本题中要求第一象限,这样就应该有0<a<π,设P为(2cosa,sina)这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和,对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa 这样四边形的面积S=S1+S2=sina+cosa也就相当于求解sina+cosa的最大值,0<a<π,sina+cosa=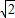 sin(a+
sin(a+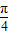 )这样其最大值就应该为
)这样其最大值就应该为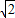 ,并且当且仅当a=
,并且当且仅当a=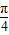 时成立.
时成立.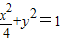 上的在第一象限内的点,
上的在第一象限内的点,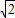 sin(a+
sin(a+ )
)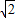 ,
,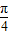 时成立.所以,面积最大值
时成立.所以,面积最大值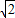 .
.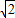 .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源:深圳市远恒佳教育集团龙华中英文实验学校高中部2006~2007学年度第一学期第1学段质量检测题高三数学(文) 题型:022
已知点P是椭圆![]() 上的在第一象限内的点,又A(2,0)、B(0,1),
上的在第一象限内的点,又A(2,0)、B(0,1),
O是原点,则四边形OAPB的面积的最大值是________
查看答案和解析>>
科目:高中数学 来源:聊城一中东校高三第一次期末数学模拟考试 题型:022
已知点P是椭圆![]() 上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是________.
上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省长沙市长郡中学高二(下)期末数学试卷(文科)(解析版) 题型:填空题
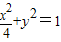 上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是 .
上的在第一象限内的点,又A(2,0)、B(0,1),O是原点,则四边形OAPB的面积的最大值是 .查看答案和解析>>
科目:高中数学 来源:2010年湖南省高考数学考前冲刺试卷(解析版) 题型:解答题
 是椭圆
是椭圆 上一点,F1、F2分别是椭圆的左、右焦点,点Q在F1P上,且|PQ|=|PF2|,则Q点坐标为 .
上一点,F1、F2分别是椭圆的左、右焦点,点Q在F1P上,且|PQ|=|PF2|,则Q点坐标为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com