
(09年海淀区二模理)(14分)
如图,斜三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() ,点
,点![]() 在底面
在底面![]() 上的射影恰好是
上的射影恰好是![]() 的中点,且
的中点,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]()
![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.

解析:(Ⅰ)证明:设![]() 的中点为
的中点为![]() .
.

在斜三棱柱![]() 中,点
中,点![]() 在底面
在底面![]() 上的射影恰好是
上的射影恰好是![]() 的中点,
的中点,
![]() 平面ABC. ……………………1分
平面ABC. ……………………1分
![]()
![]() 平面
平面![]() ,
,
![]() . ……………………2分
. ……………………2分
![]()
![]() ,
,
∴![]() .
.
![]()
![]() ,
,
∴![]() 平面
平面![]() . ……………………4分
. ……………………4分
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() . …………………………5分
. …………………………5分
解法一:(Ⅱ)连接![]() ,
,![]()
![]() 平面
平面![]() ,
,
![]() 是直线
是直线![]() 在平面
在平面![]() 上的射影. …………………………5分
上的射影. …………………………5分
![]()
![]() ,
,
![]() 平行四边形
平行四边形![]() 是菱形.
是菱形.
![]() . ………………………………………7分
. ………………………………………7分
![]() . ……………………………………9分
. ……………………………………9分
(Ⅲ)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() ,
,![]()

![]() 平面
平面![]() .
.
![]() .
.
![]() 是二面角
是二面角![]() 的平面角. …………………11分
的平面角. …………………11分
设![]() ,则
,则![]()
![]()
![]() ,
,
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.
![]() .
.
在![]() 中,可求
中,可求![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
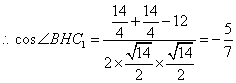 . ……………………………………13分
. ……………………………………13分
![]() .
.
∴二面角![]() 的大小为
的大小为![]() . …………………………14分
. …………………………14分
解法二:(Ⅱ)因为点![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中点,设
的中点,设![]() 的中点为
的中点为![]() ,则
,则![]() 垂直平面ABC.以
垂直平面ABC.以![]() 为原点,过
为原点,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系.
轴,建立如图所示的空间直角坐标系.

设![]() ,由题意可知,
,由题意可知,![]() .
.
设![]() ,由
,由![]() ,得
,得![]() ……………………………7分
……………………………7分
![]() .
.
又![]() .
.
![]() .
.
![]() . ………………………………………9分
. ………………………………………9分
(Ⅲ)设平面![]() 的法向量为
的法向量为![]() .
.
则
∴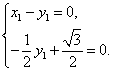
![]() .
.
设平面![]() 的法向量为
的法向量为![]() .则
.则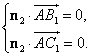
∴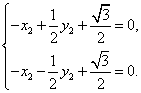
![]() . ……………………………………12分
. ……………………………………12分
![]() . …………………………………13分
. …………………………………13分
![]() 二面角
二面角![]() 的大小为
的大小为![]() . ………………………………………14分
. ………………………………………14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年海淀区二模理)(14分)已知![]() 定义域为
定义域为![]() ,满足:
,满足:
①![]() ;
;
②对任意实数![]() ,有
,有![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)求![]()
![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区二模理)(13分)
已知抛物线C:![]() ,过定点
,过定点![]()
![]() ,作直线
,作直线![]() 交抛物线于
交抛物线于![]() (点
(点![]() 在第一象限).
在第一象限).
(Ⅰ)当点A是抛物线C的焦点,且弦长![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .求证:点B的坐标是
.求证:点B的坐标是![]() 并求点
并求点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年海淀区二模理)(13分)
检测部门决定对某市学校教室的空气质量进行检测,空气质量分为A、B、C三级. 每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格. 设各教室的空气质量相互独立,且每次检测的结果也相互独立. 根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为![]() .
.
(Ⅰ)在该市的教室中任取一间,估计该间教室的空气质量合格的概率;
(Ⅱ)如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com