
设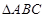 的三个内角分别为
的三个内角分别为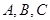 .向量
.向量 共线.
共线.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设角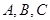 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
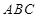 的形状.
的形状.
(Ⅰ)C=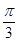 ;(Ⅱ)△
;(Ⅱ)△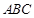 为等边三角形
为等边三角形
【解析】
试题分析:(Ⅰ)∵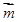 与
与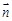 共线,∴
共线,∴ 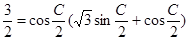
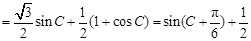 3分
3分
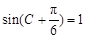 ∴C=
∴C=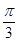 6分
6分
(Ⅱ)由已知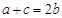 根据余弦定理可得:
根据余弦定理可得: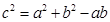 8分
8分
联立解得: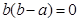
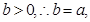
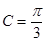 ,所以△
,所以△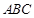 为等边三角形, 12分
为等边三角形, 12分
考点:本题考查了数量积的坐标运算及三角函数的恒等变换、余弦定理
点评:三角形的形状的判定常常通过正弦定理和余弦定理,将已知条件中的边角关系转化为纯边或纯角的关系,寻找边之间的关系或角之间关系来判定.一般的,利用正弦定理的公式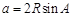 ,
,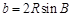 ,
,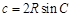 ,可将边转化为角的三角函数关系,然后利用三角函数恒等式进行化简,其中往往用到三角形内角和定理:
,可将边转化为角的三角函数关系,然后利用三角函数恒等式进行化简,其中往往用到三角形内角和定理: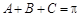 ;利用余弦定理公式
;利用余弦定理公式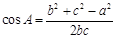 ,
,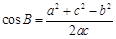 ,
,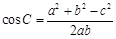 ,可将有关三角形中的角的余弦转化为边的关系,然后充分利用代数知识来解决问题.
,可将有关三角形中的角的余弦转化为边的关系,然后充分利用代数知识来解决问题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
| m |
| C |
| 2 |
| n |
| 3 |
| C |
| 2 |
| C |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| x |
| 2 |
| n |
| x |
| 2 |
| m |
| n |
| 5 |
| 13 |
| 3 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| BC |
| CA |
| CA |
| AB |
| s |
| 3 |
| t |
| C |
| 2 |
| s |
| t |
| 12 |
| 13 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海浦东高三第六次联考理科数学 题型:填空题
设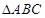 的三个内角分别为
的三个内角分别为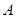 、
、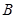 、
、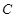 ,则下列条件中
,则下列条件中
能够确定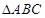 为钝角三角形的条件共有________个.
为钝角三角形的条件共有________个.
①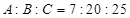 ;
;
②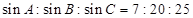 ;
;
③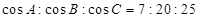 ;
;
④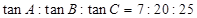 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com