在△ABC中,b=2,B=45°,若这样的三角形有两个,则a的取值范围是 .
【答案】
分析:利用正弦定理和b和sinB求得a和sinA的关系,利用B求得A+C;要使三角形两个这两个值互补先看若A≤45°,则和A互补的角大于135°进而推断出A+B>180°与三角形内角和矛盾;进而可推断出45°<A<135°若A=90,这样补角也是90°,一解不符合题意进而可推断出sinA的范围,利用sinA和a的关系求得a的范围.
解答:解:
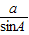
=
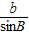
=2
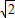
∴a=2
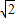
sinA
A+C=180°-45°=135°
A有两个值,则这两个值互补
若A≤45°
则和A互补的角大于135°
这样A+B>180°,不成立
∴45°<A<135°
又若A=90,这样补角也是90°,一解
所以
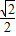
<sinA<1
a=2
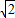
sinA
所以2<a<2
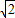
故答案为:(2,2
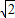
)
点评:本题主要考查了正弦定理的应用.解三角形与不等式的综合.考查了学生综合分析问题和基本的运算能力.

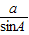 =
=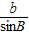 =2
=2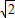
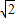 sinA
sinA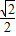 <sinA<1
<sinA<1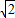 sinA
sinA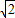
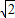 )
)

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案