Question

在△ABC中，若b²tanA=a²tanB，则△ABC的形状是（ ）
A．直角三角形
B．等腰或直角三角形
C．等腰三角形
D．等边三角形

Answer 1

【答案】分析：三角形ABC中，利用正弦定理化简a²tanB=b²tanA，再利用二倍角的正弦即可得到sin2A=sin2B，从而得到：A=B或A+B=，问题即可解决．
解答：解：∵三角形ABC中，a²tanB=b²tanA，
∴由正弦定理得：，
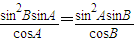
∵sinA•sinB＞0，
所以sin2A=sin2B，又A、B为三角形中的角，
∴2A=2B或2A=π-2B，
∴A=B或A+B=．
故选B．
点评：本题考查三角形的形状判断，着重考查正弦定理的应用及二倍角的正弦及诱导公式，属于中档题．