
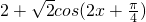 的图象向左平移m个单位(m>0),得到的图象关于直线
的图象向左平移m个单位(m>0),得到的图象关于直线 对称.
对称.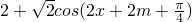 …(2分)
…(2分) 对称,
对称,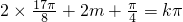 ,k∈Z…(4分)
,k∈Z…(4分)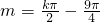 ,…(5分)
,…(5分) …(6分)
…(6分)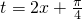 ,0<x<π,则
,0<x<π,则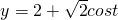 ,
,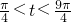 …(7分)
…(7分)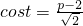 在
在 内有两个不相等的实根,…(8分)
内有两个不相等的实根,…(8分)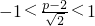 ,且
,且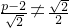 ,…(11分)
,…(11分) 且p≠3…(12分)
且p≠3…(12分)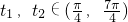 时t1+t2=2π;当
时t1+t2=2π;当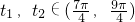 时t1+t2=4π.
时t1+t2=4π.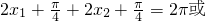
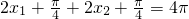 …(13分)
…(13分)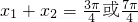 …(14分)
…(14分)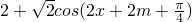 ,又由三角函数在其对称轴处取得最值,可得
,又由三角函数在其对称轴处取得最值,可得 时,y=
时,y=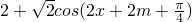 取得最值,即可得m所有可能值,进而可求m的最小值;
取得最值,即可得m所有可能值,进而可求m的最小值;

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广西桂林十八中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com