Question

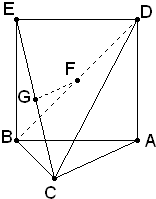
如图，三角形ABC中，AC=BC=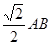，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．

（１）求证：GF//底面ABC；

（２）求证：AC⊥平面EBC；

（３）求几何体ADEBC的体积V．

 

 

 

Answer 1

【答案】

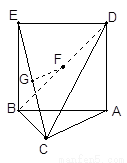
（I）证法一：连结AE，∵ADEB为正方形，F是BD中点，

∴AE∩BD=F，F是AE中点………………2分

∴GF//AC，又AC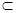平面ABC，GF 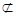平面ABC

∴GF//平面ABC………………5分

 

 

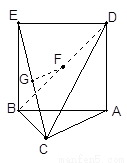
（Ⅱ）∵ADEB为正方形，∴EB⊥AB  

又∵平面ABED⊥平面ABC，交线为AB

∴BE⊥平面ABC                                           ……………… 7分

∴BE⊥AC   又∵CA²+CB²=AB²∴AC⊥BC,     

∵BC∩BE=B,

∴AC⊥平面BCE  …                                       ………………9分

（Ⅲ）取AB的中点N连结CN，

因为AC=BC，∴CN⊥AB，                                  ………………10分

又平面ABED⊥平面ABC，CN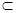平面ABC，∴CN⊥平面ABED。 11分

∵三角形ABC是等腰直角三角形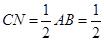，∴，         ………………12分

∵C—ABED是四棱锥,

∴V_C—ABED=                 

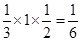
【解析】略