
 )、B(2,2)分别作抛物线的切线,两条切线交于点M.
)、B(2,2)分别作抛物线的切线,两条切线交于点M.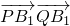 ∈(0,4]时,求直线PQ的斜率k的取值范围.
∈(0,4]时,求直线PQ的斜率k的取值范围. x2,
x2, )的切线方程为y-
)的切线方程为y- =-(x+1),
=-(x+1), ,-1),
,-1), n=1且4m-4n=1,
n=1且4m-4n=1, ,n=1,
,n=1, x2-y2=1,
x2-y2=1,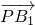 =(-x1,1-y1),
=(-x1,1-y1), =(-x2,1-y2),
=(-x2,1-y2),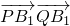 =x1x2+1-(y1+y2)+y1y2∈(0,4].
=x1x2+1-(y1+y2)+y1y2∈(0,4]. ,
, -k2)x2+2kx-2=0
-k2)x2+2kx-2=0 -k2)>0
-k2)>0 ,x1x2=
,x1x2=
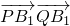 =x1x2+1-(y1+y2)+y1y2
=x1x2+1-(y1+y2)+y1y2 ,x1x2=
,x1x2= 代入,
代入,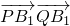 =
=
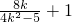

 .
.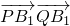 =
= ∈(0,4],
∈(0,4], ≤4,
≤4,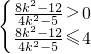
 ,
, ,或
,或 ,
,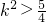 ,
,
 )∪[-1,1]∪(
)∪[-1,1]∪( ).
). x2,知y'=x,切于点A(-1,
x2,知y'=x,切于点A(-1, )的切线方程为y-
)的切线方程为y- =-(x+1),切于点B(2,2)的切线方程为y-2=2(x-2),联立解得M(
=-(x+1),切于点B(2,2)的切线方程为y-2=2(x-2),联立解得M( ,-1),由|BA|=|BM|,能够证明∠BAM=∠BMA.
,-1),由|BA|=|BM|,能够证明∠BAM=∠BMA. n=1且4m-4n=1,故m=
n=1且4m-4n=1,故m= ,n=1,双曲线方程为
,n=1,双曲线方程为 x2-y2=1.设B1(0,1),B2(0,-1),设P(x1,y1),Q(x2,y2),故
x2-y2=1.设B1(0,1),B2(0,-1),设P(x1,y1),Q(x2,y2),故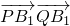 =x1x2+1-(y1+y2)+y1y2∈(0,4],设直线PQ的方程为y=kx-1(k必存在),再由根的判别式和韦达定理能求出直线PQ的斜率k的取值范围.
=x1x2+1-(y1+y2)+y1y2∈(0,4],设直线PQ的方程为y=kx-1(k必存在),再由根的判别式和韦达定理能求出直线PQ的斜率k的取值范围.

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| PB1 |
| QB1 |
查看答案和解析>>
科目:高中数学 来源:成都二模 题型:解答题
| 1 |
| 2 |
| PB1 |
| QB1 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆十一中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com