
设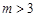 ,对于数列
,对于数列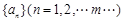 ,令
,令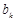 为
为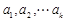 中的最大值,称数列
中的最大值,称数列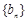 为
为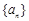 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列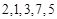 的递进上限数列为2,2,3,7,7.则下面命题中( )
的递进上限数列为2,2,3,7,7.则下面命题中( )
①若数列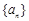 满足
满足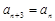 ,则数列
,则数列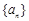 的递进上限数列必是常数列
的递进上限数列必是常数列
②等差数列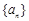 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列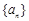 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
A.0 B.1 C.2 D.3
科目:高中数学 来源:2011-2012学年上海市青浦区高三上学期期终学习质量调研测试数学试卷 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.
考查自然数 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.
(1)若 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;
(2)是否存在数列 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
(3)是否存在数列 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省瓦房店市高一下学期期末联考理科数学 题型:选择题
设 ,对于数列
,对于数列 ,令
,令 为
为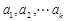 中的最大值,称数列
中的最大值,称数列 为
为 的
的
“递进上限数列”。例如数列 的递进上限数列为2,2,3,7,7.则下面命题中
的递进上限数列为2,2,3,7,7.则下面命题中
①若数列 满足
满足 ,则数列
,则数列 的递进上限数列必是常数列;
的递进上限数列必是常数列;
②等差数列 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
A. 0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题12分)
设![]() ,对于有穷数列
,对于有穷数列![]() (
(![]() …,
…,![]() ), 令
), 令![]() 为
为![]() …,
…,![]() 中的最大值,称数列
中的最大值,称数列![]() 为
为![]() 的“创新数列”. 数列
的“创新数列”. 数列![]() 中不相等项的个数称为
中不相等项的个数称为![]() 的“创新阶数”. 例如数列
的“创新阶数”. 例如数列![]() 的创新数列为2,2,3,7,7,创新阶数为3.
的创新数列为2,2,3,7,7,创新阶数为3.
考察自然数![]() …,
…,![]()
![]() 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列![]() .
.
(Ⅰ)若![]() , 写出创新数列为3,4,4,5,5的所有数列
, 写出创新数列为3,4,4,5,5的所有数列![]() ;
;
(Ⅱ) 是否存在数列![]() ,使它的创新数列为等差数列?若存在,求出所有的数列
,使它的创新数列为等差数列?若存在,求出所有的数列![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年辽宁省瓦房店市高级中学高一下学期期末联考理科数学 题型:单选题
设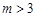 ,对于数列
,对于数列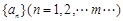 ,令
,令 为
为 中的最大值,称数列
中的最大值,称数列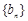 为
为 的“递进上限数列”。例如数列
的“递进上限数列”。例如数列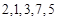 的递进上限数列为2,2,3,7,7.则下面命题中
的递进上限数列为2,2,3,7,7.则下面命题中
①若数列 满足
满足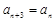 ,则数列
,则数列 的递进上限数列必是常数列;
的递进上限数列必是常数列;
②等差数列 的递进上限数列一定仍是等差数列
的递进上限数列一定仍是等差数列
③等比数列 的递进上限数列一定仍是等比数列
的递进上限数列一定仍是等比数列
正确命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com