
| A. | (-1,-$\frac{1}{2}$) | B. | [-1,-$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,0) | D. | [-$\frac{1}{2}$,0) |
分析 方法一、由函数f(x)有且仅有两个零点,等价于方程(2a+1)ex=a$\sqrt{2x+1}$有两个不等的实数根,讨论a=0和a≠0时,问题等价于两曲线有两个交点问题,再根据函数的导数判断单调性,从而求出a的取值范围.
方法二、由函数f(x)有且仅有两个零点,等价于方程(2a+1)ex=a$\sqrt{2x+1}$有两个不等的实数根,讨论a=0和a≠0时,利用函数思想研究该方程根的情况,从而求出a的取值范围.
解答 解法一、函数f(x)=(2a+1)ex-a$\sqrt{2x+1}$有且仅有两个零点,
等价于方程(2a+1)ex=a$\sqrt{2x+1}$有两个不等的实数根,
当a=0时,不满足题意;
当a≠0时,问题等价于直线y=$\frac{2a+1}{a}$与y=$\frac{\sqrt{2x+1}}{{e}^{x}}$有两个交点,
令g(x)=$\frac{\sqrt{2x+1}}{{e}^{x}}$,则g′(x)=$\frac{-2x}{{e}^{x}\sqrt{2x+1}}$,
所以当-$\frac{1}{2}$<x<0时,g′(x)>0,函数g(x)单调递增;
当x>0时,g′(x)<0,函数g(x)单调递减;
所以当x=0时,g(x)取得最大值1;
又因为g(-$\frac{1}{2}$)=0,当x>-$\frac{1}{2}$时,g(x)>0,且当x→+∞时,g(x)→0,
所以0<$\frac{2a+1}{a}$<1,解得-1<a<-$\frac{1}{2}$.
解法二、函数f(x)=(2a+1)ex-a$\sqrt{2x+1}$有且仅有两个零点,
等价于方程(2a+1)ex=a$\sqrt{2x+1}$(*)有两个不等的实数根,
当a=0时,不满足题意;
当a≠0时,方程可化为$\frac{2a+1}{a}$=$\frac{\sqrt{2x+1}}{{e}^{x}}$,
(1)若x=-$\frac{1}{2}$,则a=-$\frac{1}{2}$,不合题意;
(2)若x>-$\frac{1}{2}$,方程(*)可化为ln($\frac{2a+1}{a}$)=$\frac{1}{2}$ln(2x+1)-x,
即2ln($\frac{2a+1}{a}$)=ln(2x+1)-2x;
令h(x)=ln(2x+1)-2x,(x>-$\frac{1}{2}$),
则h′(x)=$\frac{2}{2x+1}$-2=$\frac{-4x}{2x+1}$;
当-$\frac{1}{2}$<x<0时,h′(x)>0,h(x)单调递增;
当x>0时,h′(x)<0,h(x)单调递减;
所以当x=0时,h(x)取得最大值0,
又当x→-$\frac{1}{2}$时,g(x)→-∞,
当x→+∞时,g(x)→-∞,
所以2ln($\frac{2a+1}{a}$)<0,
所以0<$\frac{2a+1}{a}$<1,
解得-1<a<-$\frac{1}{2}$.
故选:A.
点评 本题考查了函数的零点与方程的应用问题,也考查了转化问题与分类讨论思想的应用问题,是综合性题目.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | an=($\sqrt{2}$)n-1 | B. | an=($\sqrt{2}$)n | ||
| C. | an=$\left\{\begin{array}{l}{(\sqrt{2})^{n},n为奇数}\\{(\sqrt{2})^{n-1},n为偶数}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{(\sqrt{2})^{n-1},n为奇数}\\{(\sqrt{2})^{n},n为偶数}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
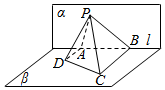 如图,已知平面α⊥β,α∩β=l,A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD、PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是( )
如图,已知平面α⊥β,α∩β=l,A、B是直线l上的两点,C、D是平面β内的两点,且DA⊥l,CB⊥l,AD=3,AB=6,CB=6,P是平面α上的一动点,且直线PD、PC与平面α所成角相等,则二面角P-BC-D的余弦值的最小值是( )| A. | $\frac{1}{\sqrt{5}}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知SA⊥正方形ABCD所在平面,O为AC与BD的交点.
如图所示,已知SA⊥正方形ABCD所在平面,O为AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}\overrightarrow{AC}$+$\frac{1}{3}$$\overrightarrow{AB}$ | B. | $\frac{1}{2}\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{AB}$ | C. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{1}{2}\overrightarrow{AB}$ | D. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{3}{2}$$\overrightarrow{AB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)∉P,h(x)∈P | B. | g(x)∈P,h(x)∈P | C. | g(x)⊆P,h(x)⊆P | D. | g(x)∈P,h(x)∉P |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12.5% | B. | 50% | C. | 75% | D. | 87.5% |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com