练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    二面角α—a—β的平面角为120°，在面α内，AB⊥a于B，AB=2在平面β内，CD⊥a

        于D，CD=3，BD=1，M是棱a上的一个动点，则AM+CM的最小值为     

                       。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，在梯形ABCD中，AB∥C，AD=DC=CB=1，∠ABC═60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
    （1）求证：BC⊥平面ACFE；
    （2）求二面角A-BF-C的平面角的余弦值；
    （3）若点M在线段EF上运动，设平MAB与平FCB所成二面角的平面角为θ（θ≤90°），试求cosθ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2004•朝阳区一模）如图，已知PA垂直于正方形ABCD所在的平面，E、F分别为AB、PD的中点，过AE、AF的平面交PC于点H，二面角P-CD-B为45°，PA=a．
    （Ⅰ）求证：AF∥EH；
    （Ⅱ）求证：平面PCE⊥平面PCD； 
    （Ⅲ）求多面体ECDAHF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•虹口区二模）（理）已知正方形ABCD的边长为1，PD⊥平面ABCD，PD=3，
    （1）若E是棱PB上一点，过点A、D、E的平面交棱PC于F，求证：BC∥EF；
    （2）求二面角A-PB-D的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

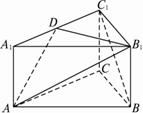
    如图所示,正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为,若经过对角线AB1且与对角线BC1平行的平面交上底面一边A1C1于点D.

    (1)确定点D的位置,并证明你的结论;

    (2)求二面角A1 –AB-1D的大小.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年甘肃省河西五市高三第一次联考数学理卷 题型：选择题

    ．下列四个命题

    ① 分别和两条异面直线均相交的两条直线一定是异面直线．  

    ② 一个平面内任意一点到另一个平面之距离均相等，那么这两个平面平行．

    ③ 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，则这两个二面角的平

    面角相等或互补．   

    ④ 过两异面直线外一点能作且只能作出一条直线和这两条异面直线同时相交．其中正确命

    题的个数是 

    A．1   B．2               C．3          D．4

     

    查看答案和解析>>

    同步练习册答案