
科目:高中数学 来源: 题型:选择题
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过38,则该塔形中正方体的个数至少是( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
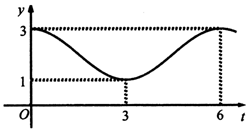 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 41 | C. | 82 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com