
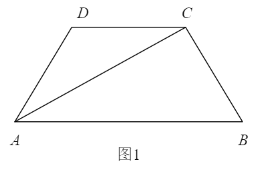
【题目】如图1,四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E为AB的中点,连接DE,DB(如图2).
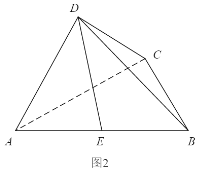
(1)求证:BC⊥AD
(2)求直线DE与平面BCD所成的角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明AC⊥BC,结合平面ADC⊥平面ABC,推导出BC⊥平面ADC,然后证明BC⊥AD;
(2)取AC中点F,连结DF,EF,得到FA,FE,FD两两垂直,以FA,FE,FD所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出它们的法向量,设直线DE与平面BCD所成角为θ,利用向量求线面角即可.
(1)在图1中,作CH⊥AB于H,
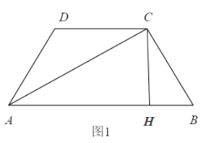
则BH![]() ,AH
,AH![]() ,
,
∵BC=2,
∴CH![]() ,CA
,CA![]() ,所以
,所以![]() ,
,
∴AC⊥BC,
∵平面ADC⊥平面ABC,且平面ADC∩平面ABC=AC,
∴BC⊥平面ADC,
又AD平面ADC,
∴BC⊥AD.
(2)取AC中点F,连结DF,FE,
由题意知FA,FE,FD两两垂直,
以FA,FE,FD所在直线分别为x,y,z轴,建立空间直角坐标系,如图,
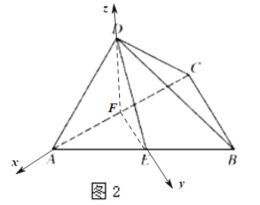
E(0,![]() ,0),D(0,0,
,0),D(0,0,![]() ),C(
),C(![]() ,0,0),
,0,0),
![]() (0,
(0,![]() ),
),![]() (0,﹣2,0),
(0,﹣2,0),![]() (
(![]() ,0,
,0,![]() ),
),
设![]() (x,y,
(x,y,
则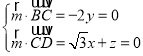 ,取x=1,
,取x=1,![]() (1,0,
(1,0,![]() ),
),
设直线DE与平面BCD所成的角为θ,
则sinθ=![]()
![]() ,
,
∴直线DE与平面BCD所成角的正弦值为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题:有厚墙![]() 尺,两只老鼠从墙的两边相对分别打洞穿墙大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问两天后,两鼠间距_______尺,两鼠相遇时,大鼠共穿了______尺墙.
尺,两只老鼠从墙的两边相对分别打洞穿墙大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问两天后,两鼠间距_______尺,两鼠相遇时,大鼠共穿了______尺墙.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正项数列![]() 的首项为
的首项为![]() ,且当数列
,且当数列![]() 是公比为
是公比为![]() 的等比数列时,则称数列
的等比数列时,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:数列
,证明:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若数列![]() 为“
为“![]() 数列”,且对任意
数列”,且对任意![]() ,
,![]() 、
、![]() 、
、![]() 成等差数列,公差为
成等差数列,公差为![]() .
.
①求![]() 与
与![]() 间的关系;
间的关系;
②若数列![]() 为递增数列,求
为递增数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(1)求C1的极坐标方程,并求C1与C2交点的极坐标![]() ;
;
(2)若曲线C3:θ=β(ρ>0)与C1,C2的交点分别为M,N,求|OM||ON|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,A、B、C、D四地新增疑似病例数据信息如下:
A地:中位数为2,极差为5; B地:总体平均数为2,众数为2;
C地:总体平均数为1,总体方差大于0; D地:总体平均数为2,总体方差为3.
则以上四地中,一定符合没有发生大规模群体感染标志的是_______(填A、B、C、D)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在
猜想”,是德国数学家洛萨克拉茨在![]() 年世界数学家大会上公布的一个猜想:任给一个正整数
年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘
为奇数就将它乘![]() 加
加![]() ,不断重复这样的运算,经过有限步后,最终都能够得到
,不断重复这样的运算,经过有限步后,最终都能够得到![]() ,得到
,得到![]() 即终止运算,己知正整数
即终止运算,己知正整数![]() 经过
经过![]() 次运算后得到
次运算后得到![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com