Question

要使不等式mx²+mx+2＞0对于一切实数x均成立，则m的取值范围是    ．

Answer 1

【答案】分析：当m≠0时，mx²+mx+2＞0对于一切x恒大于零的充要条件是，当m=0时，原不等式为2＞0，显然对一切x恒成立．由此能够求出不等式对一切实数x恒成立的m的取值范围．
解答：解：①当m≠0时，
mx²+mx+2＞0对于一切x恒大于零的充要条件是
，
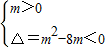
解得0＜m＜8．
②当m=0时，原不等式为2＞0，显然对一切x恒成立．
综上可得，
当0≤m＜8时，
不等式对一切实数x恒成立．
故答案为：[0，8）．
点评：本题考查二次函数的取值范围，是基础题．解题时要认真审题，注意分类讨论思想的灵活运用．