


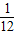
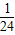
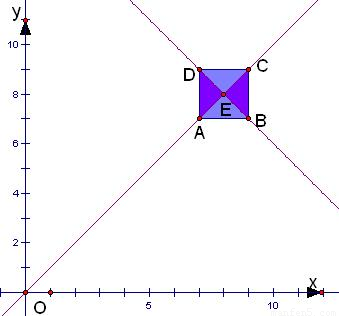
 解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数
解:∵a从区间[7,9]中任取一个数,b从区间[7,9]中任取一个数 ×2×2=2
×2×2=2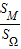 =
= .
.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省南通市通州区高三(下)2月寒假调研数学试卷(解析版) 题型:解答题
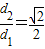 .
.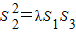 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港市梁丰高级中学高三(上)期末数学模拟试卷(一)(解析版) 题型:解答题
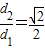 .
.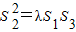 成立.若存在,求出λ的值;若不存在,请说明理由.
成立.若存在,求出λ的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:解答题
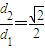 .
.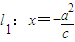 、点F(-c,0)、曲线C:
、点F(-c,0)、曲线C: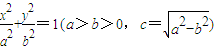 ,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).
,则使等式S22=λS1S3成立的λ的值仍保持不变.请给出你的判断______ (填写“不正确”或“正确”)(限于时间,这里不需要举反例,或证明).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com