
 如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.
如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论. 分析 作出辅助线BM、AM、FH,把求∠HAF的度数等价转化为求其全等三角形的对应角∠MAF的度数.
解答 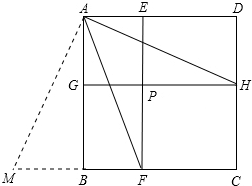 解:如图,连结FH,延长CB到M,使BM=DH,连结AM,
解:如图,连结FH,延长CB到M,使BM=DH,连结AM,
∵Rt△ABM≌Rt△ADH,∴AM=AH,∠MAB=∠HAD,
∴∠MAH=∠MAB+∠BAH=∠BAH+∠HAD=90°,
如图,设正方形ABCD边长为a,AG=m,GP=n,则FC=a-n,CH=a-m,
∵矩形PFCH的面积恰好是矩形AGPE面积的2倍,
∴a2-(m+n)a+mn=2mn,①
在Rt△FCH中,FH2=(a-n)2+(a-m)2,②
联立①②,得FH2=MF2=(m+n)2,∴FH=MF.
∵AF=AF,AH=AM,∴△AMF≌△HAF,
∴∠HAF=∠MAF=45°.
点评 本题考查满足条件的角的大小的确定并证明,是中档题,解题时要注意全等三角形的判定定理的合理运用,构建全等三角形并进行证明是解题的关键.


科目:高中数学 来源: 题型:解答题
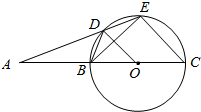 已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.
已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
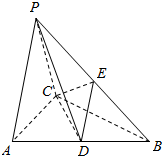 三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.
三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
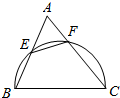 如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
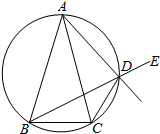 已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.
已知△ABC中,AB=AC,D是△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
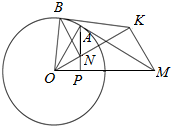 如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.
如图,过圆O外一点M作圆的切线,切点为A,过A作AP⊥OM于P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com