
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式,并用分段函数的形式给出;
(2)作出函数f(x)的简图;
(3)写出函数f(x)的单调区间及最值.
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,an+1 ![]() =1,记Sn=a12+a22+…+an2 , 若S2n+1﹣Sn≤
=1,记Sn=a12+a22+…+an2 , 若S2n+1﹣Sn≤ ![]() 对任意n∈N*恒成立,则正整数m的最小值是 .
对任意n∈N*恒成立,则正整数m的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x≤﹣1或x≥5},集合B={x|2a≤x≤a+2}.
(1)若a=﹣1,求A∩B和A∪B;
(2)若A∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
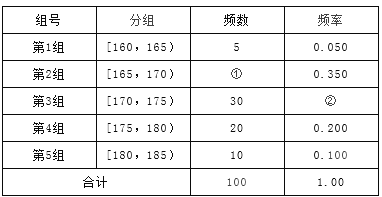
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
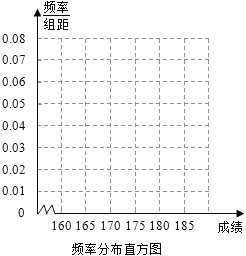
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加5个单位;③线性回归方程
平均增加5个单位;③线性回归方程![]() 必过
必过![]() ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
A.0 B.1 C. 2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2![]() sinxcosx+2cos2x﹣1.
sinxcosx+2cos2x﹣1.
(1)求f(x)的最大值,以及该函数取最大值时x的取值集合;
(2)在△ABC中,a、b、c分别是角A、B、C所对的边长,且![]() ,求角C.
,求角C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com