练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知圆C：(x+1)2+y2=r2(r为常数，且r＞2)，定点B(1，0),A是圆C上的动点，直线AC与线段朋的垂直平分线l相交于点M．当点A在圆C上移动一周时，点M的轨迹记为曲线F．

    (1)求曲线F的方程；

    (2)若点M在第一象限，且=,△CMB的面积S△CMB=，求r的值及直线l的方程．

    解：(1)连接MB，由题意有：

    |MC|+|MB|=|MC|+|MA|=|AC|=r

    又r＞|BC|=2

    ∴点M的轨迹是以C(-1，0)，B(1，0)为焦点的椭圆

    ∴a=  c=l

    ∴曲线F的方程为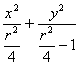：=1

    (2)设M(x0，y0)，且x0、y0＞0

    由于S△CMB=|CB|y0=y0=  所以M(x0，)

    又=(x0+1，)，=(x0-1，)

    所以·=

    所以x0=1，即M(1，)

    所以|MC|=,|MB|=

    所以r=|MC|+|MB|=4

    (或用待定系数法将M(1，)代入(1)中方程解出r)

    点A分线段CM所成定比λ=．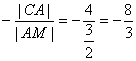

    即点A坐标x=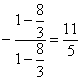,y=.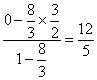

    所以点A(,)

    (或求出直线AC方程与圆C方程联立求出点A坐标)

    所以KAB=/(-1)=2，又l⊥AB所以kl=

    故直线l方程为：y- (x-1)即x+2y-4=0

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知圆C：
    x=1+cosθ
    y=sinθ
    （θ为参数）和直线l：
    x=2+tcosα
    y=
    		3
    +tsinα
    （其中为参数，α为直线的倾斜角），如果直线与圆C有公共点，求α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C：(x+1)2+(y-
    		3
    )2=1    ，则圆心C的极坐标为
    (2， 
    2π
    3
    )
    (2， 
    2π
    3
    )
     （ρ＞0，0≤θ＜2π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C：
    x=1+cosθ
    y=sinθ
    （θ为参数）和直线θl：
    x=2++tcosα
    y=
    		3
    +tsinα
    （其中t为参数，α为直线l的倾斜角）
    （1）当α=
    2π
    3
    时，求圆上的点到直线l的距离的最小值；
    （2）当直线l与圆C有公共点时，求α的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C：(x-1)2+y2=9内有一点P(2，2)，过点P作直线l交圆C于A、B两点.

    (1)当l经过圆心C时，求直线l的方程；

    (2)当弦AB被点P平分时，写出直线l的方程；

    (3)当直线l的倾斜角为45°时，求弦AB的长.

    查看答案和解析>>

    科目：高中数学 来源：2014届湖南省华容县高一第一学期期末考试数学试卷 题型：解答题

    (本小题满分8分)已知圆c：(x-1)2＋y2＝4，直线l：mx－y－1＝0

    (1)当m＝–1时，求直线l圆c所截的弦长；

    (2)求证：直线l与圆c有两个交点。

     

    查看答案和解析>>

    同步练习册答案