
已知数列an=n-16,bn=(-1)n|n-15|,其中n∈N*.
(1)求满足an+1=|bn|的所有正整数n的集合;
(2)若n≠16,求数列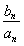 的最大值和最小值;
的最大值和最小值;
(3)记数列{anbn}的前n项和为Sn,求所有满足S2m=S2n(m<n)的有序整数对(m,n).
(1){n|n≥15,n∈N*}(2)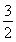 (n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8
(n=18),最小值-2(n=17)(3)S16=S14,m=7,n=8
【解析】(1)an+1=|bn|,n-15=|n-15|.
当n≥15时,an+1=|bn|恒成立;
当n<15时,n-15=-(n-15),n=15(舍去).
∴n的集合为{n|n≥15,n∈N*}.
(2)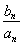 =
=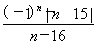 .
.
(ⅰ)当n>16时,n取偶数时,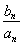 =
=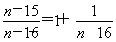 ,
,
当n=18时, =
=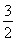 ,无最小值;n取奇数时,
,无最小值;n取奇数时,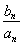 =-1-
=-1-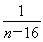 ,
,
n=17时,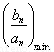 =-2,无最大值.
=-2,无最大值.
(ⅱ)当n<16时,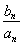 =
=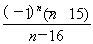 .
.
当n为偶数时,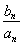 =
=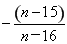 =-1-
=-1-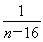 .
.
n=14时, =-
=-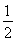 ,
,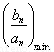 =-
=-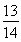 ;
;
当n为奇数时,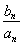 =
=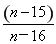 =1+
=1+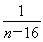 ,
,
n=1时, =1-
=1-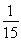 =
=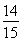 ,n=15时,
,n=15时,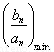 =0.
=0.
综上,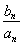 最大值为
最大值为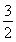 (n=18),最小值-2(n=17).
(n=18),最小值-2(n=17).
(3)当n≤15时,bn=(-1)n-1(n-15),a2k-1b2k-1+a2kb2k=2(16-2k)≥0,
当n>15时,bn=(-1)n(n-15),a2k-1b2k-1+a2kb2k=2(2k-16)>0,其中a15b15+a16b16=0,
∴S16=S14,m=7,n=8.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:填空题
a、b、c为三条不重合的直线,α、β、γ为三个不重合平面,现给出六个命题:
①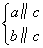 a∥b;②
a∥b;②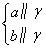 a∥b;③
a∥b;③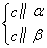 α∥β;
α∥β;
④ α∥β;⑤
α∥β;⑤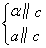 α∥a;⑥
α∥a;⑥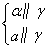 a∥α.
a∥α.
其中正确的命题是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:解答题
已知:a、b、c、d是不共点且两两相交的四条直线,求证:a、b、c、d共面
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:解答题
已知数列{an},其前n项和为Sn.
(1)若对任意的n∈N,a2n-1,a2n+1,a2n组成公差为4的等差数列,且a1=1, =2013,求n的值;
=2013,求n的值;
(2)若数列 是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+
是公比为q(q≠-1)的等比数列,a为常数,求证:数列{an}为等比数列的充要条件为q=1+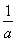 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和.若a1,a2,a5成等比数列,则S8=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=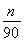 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
已知等差数列{an}的公差d=1,前n项和为Sn.
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:解答题
设f(x)=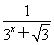 ,求f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值.
,求f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷(解析版) 题型:填空题
(1)已知等差数列{an}的公差为d(d≠0),且a3+a6+a10+a13=32.若am=8,则m=________.
(2)设等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a7+a8+a9=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com