
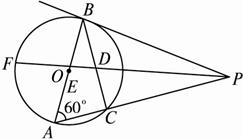
图2-4-17
(1)求证:PA·BD=PB·AE;
(2)证明⊙O的直径长为常数;
(3)求tan∠FPA的值.
思路分析:(1)由△PBD∽△PAE即可证得.?
(2)由韦达定理知AE +BD =k,只需证BE =BD,这可由角的相等证得.?
(3)要求tan∠FPA,先将∠FPA转化到直角三角形中,而∠FPB =∠FPA,∠FPB恰好在Rt△PBE中,解此三角形即可.
(1)证明:∵PB切⊙O于点B,∴∠PBD =∠A.?
又PE平分∠APB,∴∠APE =∠BPD.?
∴△PBD∽△PAE.∴![]() =
=![]() .?
.?
∴PA·BD = PB·AE.
(2)解:由(1)知∠APE =∠EPB,?
又∵∠BED =∠A +∠EPA,∠BDE =∠PBC+∠EPB,?
∴∠BED =∠BDE.∴BE =BD.?
∵AE、BD为方程x2-kx +![]() =0的两个根,?
=0的两个根,?
∴AE +BD =k =AB.?
∴⊙O的直径为常数k.
(3)解:∵PB切⊙O于点B,AB为直径,?
∴∠PBA =90°.∵∠A =60°,?
∴PB =PA·sin60°=![]() .?
.?
由(1)得PA·BD =PB·AE,?
∴![]() .?
.?
∵AE、BD的长是方程x2-kx +![]() =0的两个根,
=0的两个根,
∴AE·BD =![]() .?
.?
∴AE =2,BD =![]() ∴
∴![]() .?
.?
在Rt△PBA中,PB =AB·tan60°=(![]() )·
)·![]() =
=![]() .?
.?
在Rt△PBE中,tan∠BPE =![]() =
=![]() =
=![]() ,?
,?
又∠FPA =∠BPF,∴tan∠FPA =![]() .
.


科目:高中数学 来源:全优设计必修二数学苏教版 苏教版 题型:038
如图所示,根据指令(r,![]() )(其中r≥0,-180°<
)(其中r≥0,-180°<![]() ≤180°),机器人在平面上能完成下列动作:先原地旋转角度
≤180°),机器人在平面上能完成下列动作:先原地旋转角度![]() (
(![]() 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转![]() ;
;![]() 为负时,按顺时针方向旋转-
为负时,按顺时针方向旋转-![]() ),再朝面对的方向沿直线行走距离r.
),再朝面对的方向沿直线行走距离r.

(1)现机器人在直角坐标系的坐标原点,且面对x轴正方向.试给机器人下一个指令,使其移动到点A(4,4).
(2)机器人在完成该指令后,发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动.已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?
查看答案和解析>>
科目:高中数学 来源: 题型:013
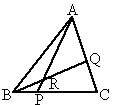
如图所示,
P、Q分别在BC和AC上,BP∶CP=2∶5,CQ∶QA=3∶4,则 =
=
[
]|
A .3∶14 |
B .14∶3 |
C .17∶3 |
D .17∶14 |
查看答案和解析>>
科目:高中数学 来源:2013届浙江省宁波市高一下期末考数学试卷 题型:选择题
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数,如
个数,如 ,
, .若
.若 ,则
,则 与
与 的和为
的和为
A. 106 B.107 C.108 D.109
1
2 4
3 5 7
6 8 10 12
9 11 13 15 17
14 16 18 20 22 24
……………………………………
(第10题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列![]() 的通项公式为
的通项公式为![]() (n
(n![]() ),现将该数列
),现将该数列![]() 的各项排列成如图的三角数阵:记
的各项排列成如图的三角数阵:记![]() 表示该数阵中第a行的第b个数,则数阵中的数2013对应于( )
表示该数阵中第a行的第b个数,则数阵中的数2013对应于( )
第1行 1
第2行 3 5
第3行 7 9 11
第4行 13 15 17 19
…………………………………
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com