解:(1)a
n+6=a
n+5-a
n-4=a
n+4-a
n+3-a
n-4
=-a
n+3=-a
n+2+a
n+1=-(a
n+1-a
n)+a
n+1=a
n,
得T=6
所以,数列{a
n}是以6为周期的周期数列,
周期为任意正整数
又由
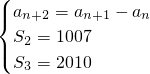
,
得a
1=2,a
2=1005,a
3=1003,a
4=-2,a
5=-1005,a
6=-1003S
6=0,
且数列{a
n}是以6为周期的周期数列,
所以,S
6n=0,
所以 S
2009=S
5=a
3=1003
(2)当p=0时,a
1=a
2=0,a
n+1=-2a
n2+2a
n=0,
即{a
n}是周期数列
当p≠0,
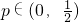
时,
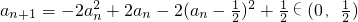
由已知
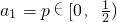
,
且a
n+1=-2a
n2+2a
n,
可得
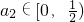
,
依此类推可得
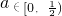
(n∈N
*)
所以 a
n+1-a
n=-2a
n2+a
n=a
n(1-2a
n)>0,所以a
n+1>a
n即数列{a
n}是递增数列,非周期数列;
(3)由(1)知,S
2=a
1+a
2=a
1+1005=1007,
所以a
1=2,a
2=1005,a
3=1003,a
4=-2,a
5=-1005,a
6=-1003,
且数列{a
n}是周期为6的周期数列,
所以(a
n)
max=1005(n∈N
*),(a
n)
min=-1005,
且 a
6n+1=2,a
6n+2=1003,a
6n+3=1005,a
6n+4=-2,
a
6n+5=-1005,a
6n+6=-1003,
而当n≥12时,
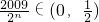
,
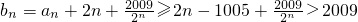
,
即2n≥2009+1005=3014
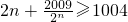
,
得n≥1507,即 n≥1507时,
都有b
n>2009;
又
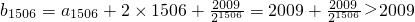
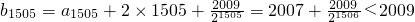
综上,存在最小的自然数n=1506,
对一切自然数m,当m≥n=1506,
都有b
m>2009.
分析:(1)a
n+6=a
n+5-a
n-4=a
n+4-a
n+3-a
n-4=-a
n+3=-a
n+2+a
n+1=-(a
n+1-a
n)+a
n+1=a
n,得T=6,由此能求出 S
2009=S
5=a
3=1003.
(2)当p=0时,a
1=a
2=0,a
n+1=-2a
n2+2a
n=0,即{a
n}是周期数列,由此能推导出数列{a
n}是递增数列,非周期数列.
(3)由S
2=a
1+a
2=a
1+1005=1007,知a
1=2,a
2=1005,a
3=1003,a
4=-2,a
5=-1005,a
6=-1003,且数列{a
n}是周期为6的周期数列,由此能推导出存在最小的自然数n=1506,对一切自然数m,当m≥n=1506,都有b
m>2009.
点评:本题考查数列和不等式的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐条件,合理地进行等价转化.

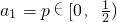 ,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;
,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;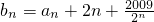 ,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.
,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.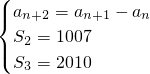 ,
,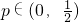 时,
时,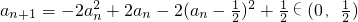
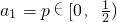 ,
,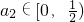 ,
,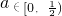 (n∈N*)
(n∈N*)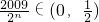 ,
,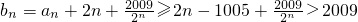 ,
,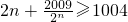 ,
,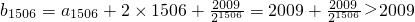
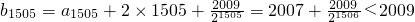


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案