
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
(1)见解析(2)t=2(3)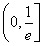 ∪[e,+∞)
∪[e,+∞)
【解析】审题引导:本题考查函数与导数的综合性质,函数模型并不复杂,(1)(2)两问是很常规的,考查利用导数证明单调性,考查函数与方程的零点问题.第(3)问要将“若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1”转化成|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1成立,最后仍然是求值域问题,但在求值域过程中,问题设计比较巧妙,因为在过程中还要构造函数研究单调性来确定导函数的正负.
规范解答:(1)证明:f′(x)=axlna+2x-lna=2x+(ax-1)·lna.(2分)
由于a>1,故当x∈(0,+∞)时,lna>0,ax-1>0,所以f′(x)>0.
故函数f(x)在(0,+∞)上单调递增.(4分)
(2)【解析】
当a>0,a≠1时,因为f′(0)=0,且f′(x)在R上单调递增,故f′(x)=0有唯一解x=0.(6分)所以x、f′(x)、f(x)的变化情况如下表所示:
x | (-∞,0) | 0 | (0,+∞) |
f′(x) | - | 0 | + |
f(x) | ? | 极小值 | ? |
又函数y=|f(x)-t|-1有三个零点,所以方程f(x)=t±1有三个根,而t+1>t-1,所以t-1=f(x)min=f(0)=1,解得t=2.(10分)
(3)【解析】
因为存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,所以当x∈[-1,1]时,|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1.(12分)
由(2)知,f(x)在[-1,0]上递减,在[0,1]上递增,所以当x∈[-1,1]时,f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)}.
而f(1)-f(-1)=(a+1-lna)-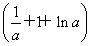 =a-
=a-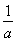 -2lna,
-2lna,
记g(t)=t- -2lnt(t>0),因为g′(t)=1+
-2lnt(t>0),因为g′(t)=1+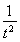 -
-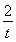 =
= ≥0(当且仅当t=1时取等号),
≥0(当且仅当t=1时取等号),
所以g(t)=t-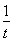 -2lnt在t∈(0,+∞)上单调递增,而g(1)=0,
-2lnt在t∈(0,+∞)上单调递增,而g(1)=0,
所以当t>1时,g(t)>0;当0<t<1时,g(t)<0,
也就是当a>1时,f(1)>f(-1);当0<a<1时,f(1)<f(-1).(14分)
①当a>1时,由f(1)-f(0)≥e-1?a-lna≥e-1?a≥e,
②当0<a<1时,由f(-1)-f(0)≥e-1?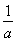 +lna≥e-1?0<a≤
+lna≥e-1?0<a≤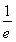 ,
,
综上知,所求a的取值范围为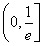 ∪[e,+∞).(16分)
∪[e,+∞).(16分)


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第4课时练习卷(解析版) 题型:解答题
已知奇函数f(x)的定义域为[-2,2],且在区间[-2,0]内递减,若f(1-m)+f(1-m2)<0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第1课时练习卷(解析版) 题型:解答题
判断下列对应是否是从集合A到集合B的函数.
(1) A=B=N*,对应法则f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,对应法则f:x→y,这里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],对应法则f:x→y,这里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,对应法则:对任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
若奇函数f(x)与偶函数g(x)满足f(x)+g(x)=2x,则函数g(x)的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
关于函数f(x)=lg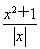 (x>0,x∈R),下列命题正确的是________.(填序号)
(x>0,x∈R),下列命题正确的是________.(填序号)
①函数y=f(x)的图象关于y轴对称;
②在区间(-∞,0)上,函数y=f(x)是减函数;
③函数y=f(x)的最小值为lg2;
④在区间(1,+∞)上,函数y=f(x)是增函数.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-ax2(a>0)的一部分,栏栅与矩形区域的边界交于点M、N,交曲线于点P,设P(t,f(t)).
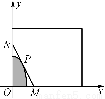
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t);
(2)若在t=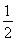 处,S(t)取得最小值,求此时a的值及S(t)的最小值.
处,S(t)取得最小值,求此时a的值及S(t)的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:填空题
某商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系为P=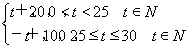 且该商品的日销售量Q与时间t(天)的函数关系为Q=-t+40(0<t≤30,t∈N),则这种商品日销量金额最大的一天是30天中的第________天.
且该商品的日销售量Q与时间t(天)的函数关系为Q=-t+40(0<t≤30,t∈N),则这种商品日销量金额最大的一天是30天中的第________天.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第11课时练习卷(解析版) 题型:填空题
一个物体的运动方程为s=1-t+t2,其中s的单位是m,t的单位是s,那么物体在3s末的瞬时速度是_______m/s.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com