
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-ax2(a>0)的一部分,栏栅与矩形区域的边界交于点M、N,交曲线于点P,设P(t,f(t)).
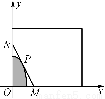
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t);
(2)若在t=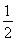 处,S(t)取得最小值,求此时a的值及S(t)的最小值.
处,S(t)取得最小值,求此时a的值及S(t)的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第3课时练习卷(解析版) 题型:填空题
函数f(x)= 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:解答题
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
已知函数f(x)=||x-1|-1|,若关于x的方程f(x)=m(m∈R)恰有四个互不相等的实根x1,x2,x3,x4,则x1x2x3x4的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=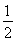 AB,tan∠FED=
AB,tan∠FED=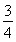 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.

(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款iPhone手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:解答题
已知函数f(x)=lnx-ax(a∈R).
(1)求函数f(x)的单调区间;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:解答题
已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求实数m的取值范围;
(2)若方程两根均在区间(0,1)内,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com