
分析 (Ⅰ)求导数,分类讨论,利用导数的正负,可得函数g(x)的单调性;
(Ⅱ)证明函数Q点处的切线斜率与直线AB斜率相等即可;
(Ⅲ)若g(x)满足(2)中结论,有$g'({x_0})=\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$,设$\frac{x_1}{x_2}=t$,则*式整理得$lnt=\frac{{2({t-1})}}{t+1}$,问题转化成该方程在(0,1)上是否有解,从而得解.
解答 (本题满分为14分)
解:(I)由题知$g'(x)=\frac{2a}{x}+2x-2=\frac{{2({{x^2}-x+a})}}{x}$,
因为$a>\frac{1}{4}$时,△<0,g'(x)>0,函数g(x)在定义域(0,+∞)上单调递增;…..(4分)
(II)g(x)=x2-2x,$g'(x)=2x-2{\left.{\;}\right|_{x={x_0}}}=2{x_0}-2$,${k_{AB}}=\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}=\frac{{({x_1}+{x_2}-2)({x_1}-{x_2})}}{{{x_1}-{x_2}}}=2{x_0}-2$,
所以函数Q点处的切线与直线AB平行; ….(7分)
(III)设A(x1,g(x1)),B(x2,g(x2))(0<x1<x2),
若g(x)满足( II)中结论,有$g'({x_0})=\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$,
即$\frac{2a}{{\frac{{{x_1}+{x_2}}}{2}}}+{x_1}+{x_2}-2=\frac{{2aln\frac{x_1}{x_2}}}{{{x_1}-{x_2}}}+{x_1}+{x_2}-2$,
即$ln\frac{x_1}{x_2}=\frac{{2({{x_1}-{x_2}})}}{{{x_1}+{x_2}}}$*….(9分)
设$\frac{x_1}{x_2}=t$,则*式整理得$lnt=\frac{{2({t-1})}}{t+1}$,问题转化成该方程在(0,1)上是否有解;…(11分)
设函数$h(t)=lnt-\frac{{2({t-1})}}{t+1}$,则$h'(t)=\frac{1}{t}-\frac{4}{{{{(t+1)}^2}}}=\frac{{{{({t-1})}^2}}}{{t{{(t+1)}^2}}}>0$,
所以函数h(t)在(0,1)单调递增,即h(t)<h(1)=0,
即方程$lnt=\frac{{2({t-1})}}{t+1}$在(0,1)上无解,
即函数g(x)不满足(2)中结论.…..(14分)
点评 本题考查导数知识的综合运用,考查函数的单调性,考查导数的几何意义,考查了转化思想的应用,考查学生分析解决问题的能力,属于难题.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x0)=0 | B. | f(x0)<0 | C. | f(x0)>0 | D. | f(x0)的符号不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | (-1,2) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^2{6^4}$ | B. | $C_5^2{6^4}$ | C. | $A_5^2A_4^4$ | D. | $C_5^2A_4^4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
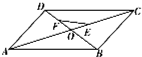
| A. | $\overrightarrow{FE}=-\frac{1}{12}\overrightarrow{AB}-\frac{1}{12}\overrightarrow{AD}$ | B. | $\overrightarrow{FE}=-\frac{1}{12}\overrightarrow{AB}-\frac{5}{12}\overrightarrow{AD}$ | C. | $\overrightarrow{FE}=\frac{5}{12}\overrightarrow{AB}-\frac{1}{12}\overrightarrow{AD}$ | D. | $\overrightarrow{FE}=\frac{5}{12}\overrightarrow{AB}-\frac{5}{12}\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40}{21}$ | B. | $\frac{41}{20}$ | C. | 2 | D. | $\frac{43}{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com