
 的椭圆C1的顶点,A1、A2恰好是双曲线
的椭圆C1的顶点,A1、A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1、A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2。
的左右焦点,点P是椭圆上不同于A1、A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2。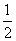 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值。
,求实数m的值。 科目:高中数学 来源: 题型:
(本小题满分13分)已知离心率为![]() 的椭圆C:
的椭圆C:![]() 的左顶点为A,上顶点为B,且点B在圆M:
的左顶点为A,上顶点为B,且点B在圆M:![]() 上.
上.
(1)求椭圆C的方程;
(2)若过点A的直线l与圆M交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省怀化三中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
 的椭圆C:
的椭圆C: 过(1,
过(1, )
)查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省赣州市南康中学高二(上)12月月考数学试卷(文科)(解析版) 题型:解答题
 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点. ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:2012年天津市武清区高考数学一模试卷(理科)(解析版) 题型:解答题
 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2010年安徽省宿州市高考数学三模试卷(文科)(解析版) 题型:解答题
 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
. .试探究
.试探究 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com