
据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
假设投资A项目的资金为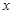 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为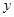 (
(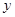 ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利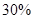 的可能性为
的可能性为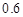 ,亏损
,亏损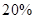 的可能性为
的可能性为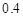 ;位于二类风区的B项目获利
;位于二类风区的B项目获利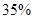 的可能性为
的可能性为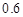 ,亏损
,亏损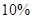 的可能性是
的可能性是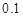 ,不赔不赚的可能性是
,不赔不赚的可能性是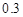 .
.
(1)记投资A,B项目的利润分别为 和
和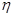 ,试写出随机变量
,试写出随机变量 与
与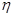 的分布列和期望
的分布列和期望 ,
,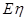 ;
;
(2)某公司计划用不超过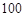 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投
资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利
润之和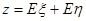 的最大值.
的最大值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2只正品,每次取一个,取出后不放回,直到取出2个正品为止.设X为取出的次数,求X的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
| 评估的平均得分 | 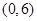 | 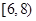 | 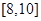 |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
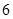 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过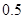 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第16届亚运会于2010年11月12日在广州举办,运动会期间来自广州大学和中山大学的共计6名大学生志愿者将被随机平均分配到跳水、篮球、体操这三个比赛场馆服务,且跳水场馆至少有一名广州大学志愿者的概率是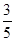 .
.
(1)求6名志愿者中来自广州大学、中山大学的各有几人?
(2)设随机变量X为在体操比赛场馆服务的广州大学志愿者的人数,求X的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
 .
. ,求
,求 的分布列,数学期望以及方差.下面的临界值表供参考:
的分布列,数学期望以及方差.下面的临界值表供参考: | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
| X1 | 5% | 10% |
| P | 0.8 | 0.2 |
| X2 | 2% | 8% | 12% |
| P | 0.2 | 0.5 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设甲、乙、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.三人各向目标射击一次,求至少有一人命中目标的概率及恰有两人命中目标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设连续掷两次骰子得到的点数分别为m、n,令平面向量a=(m,n),b=(1,-3).
(1) 求使得事件“a⊥b”发生的概率;
(2) 求使得事件“|a|≤|b|”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙等五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com