
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
 .
. ,求
,求 的分布列,数学期望以及方差.下面的临界值表供参考:
的分布列,数学期望以及方差.下面的临界值表供参考: | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
) (1)列联表补充如下
(2)有99.5%的把握认为是否患心肺疾病是与性别有关系的; 患心肺疾病 不患心肺疾病 合计 男 20 5 25 女 10 15 25 合计 30 20 50
(3) 分布列如下:
分布列如下:
0 1 2 3 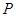
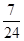
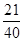
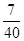
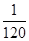
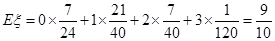
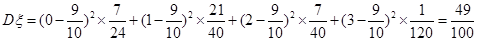 .
.
解析试题分析:(1)先由全部50人中随机抽取1人,抽到患心肺疾病的人的概率为
科目:高中数学
来源:
题型:解答题
有一批数量很大的环形灯管,其次品率为20%,对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查中止,否则继续抽查,直到抽出次品,但抽查次数最多不超过5次.求抽查次数ξ的分布列.
科目:高中数学
来源:
题型:解答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
科目:高中数学
来源:
题型:解答题
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
科目:高中数学
来源:
题型:解答题
已知某种零件的尺寸X(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在(80,+∞)上是减函数,且f(80)=
科目:高中数学
来源:
题型:解答题
据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
科目:高中数学
来源:
题型:解答题
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
科目:高中数学
来源:
题型:解答题
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件A“取出的2件产品都是二等品”的概率P(A)=0.04
科目:高中数学
来源:
题型:解答题
在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起.若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 得到患心肺疾病的总人数:
得到患心肺疾病的总人数: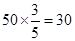 人,而女有10人,所以男有20人,进而可补充完列联表的内容;(2)先由公式
人,而女有10人,所以男有20人,进而可补充完列联表的内容;(2)先由公式 计算出
计算出 ,然后结合提供的临界值表可作出结论的判断;(3)先确定
,然后结合提供的临界值表可作出结论的判断;(3)先确定 所有可能的取值情况,然后根据超几何分布的概率计算方法得到各种取值的概率;最后由公式
所有可能的取值情况,然后根据超几何分布的概率计算方法得到各种取值的概率;最后由公式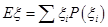 求出数学期望,由
求出数学期望,由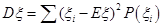 求出方差即可.
求出方差即可.
试题解析:(1)因为在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为 ,所以患心肺疾病的人共有
,所以患心肺疾病的人共有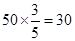 人,而女有10人,所以男有20人,从而可得列联表如下
人,而女有10人,所以男有20人,从而可得列联表如下
(2)因为 患心肺疾病 不患心肺疾病 合计 男 20 5 25 女 10 15 25 合计 30 20 50  ,所以
,所以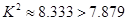 那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.
那么,我们有99.5%的把握认为是否患心肺疾病是与性别有关系的.
(3) 的所有可能取值:0,1,2,3
的所有可能取值:0,1,2,3 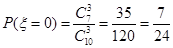
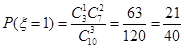
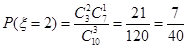
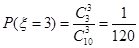
 分布列如下:
分布列如下:
0 1 2 3 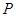


心算口算巧算系列答案
三维数字课堂系列答案
实验报告系列答案
探究活动报告册系列答案
家庭作业系列答案
课堂作业同步练习系列答案
教材完全解读系列答案
课程达标测试卷系列答案
清华绿卡核心密卷创新测试卷系列答案
小学素质强化训练AB卷系列答案
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求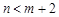 的概率.
的概率.甲
乙
9 8
8
4 8 9
2 1 0
9
 6
6
(1)求 ;
;
(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率. .
.
(1)求正态分布密度函数的解析式;
(2)估计尺寸在72mm~88mm之间的零件大约占总数的百分之几.
假设投资A项目的资金为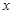 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为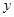 (
(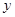 ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利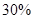 的可能性为
的可能性为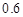 ,亏损
,亏损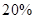 的可能性为
的可能性为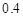 ;位于二类风区的B项目获利
;位于二类风区的B项目获利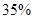 的可能性为
的可能性为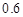 ,亏损
,亏损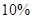 的可能性是
的可能性是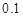 ,不赔不赚的可能性是
,不赔不赚的可能性是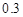 .
.
(1)记投资A,B项目的利润分别为 和
和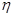 ,试写出随机变量
,试写出随机变量 与
与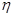 的分布列和期望
的分布列和期望 ,
,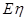 ;
;
(2)某公司计划用不超过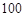 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投
资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利
润之和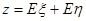 的最大值.
的最大值.
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件重量段
[80,85)
[85,90)
[90,95)
[95,100]
件数
5
a
15
b
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共10件,从中任意抽取2件;X表示取出的2件产品中二等品的件数,求X的分布列.
(1)甲、乙两单位的演出序号均为偶数的概率;
(2)甲、乙两单位的演出序号不相邻的概率.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号