Question

已知点G是圆F：(x+2)²+y²=4上任意一点，R（2，0），线段GR的垂直平分线交直线GF于H.

（1）求点H的轨迹C的方程；

（2）点M（1，0），P、Q是轨迹C上的两点，直线PQ过圆心F（-2，0），且F在线段PQ之间，求△PQM面积的最小值.

Answer 1

解：（1）点H的轨迹C的方程为x²=1.

（2）设P(x₁,y₁),Q(x₂,y₂),若PQ⊥x轴,则直线PQ:x=-2代入C的方程得y₁=3,y₂=-3,

S_△PQM=S_△PFM+S_△QFM=×6×3=9.

若PQ不垂直于x轴，设直线PQ:y=k(x+2).

∵F在P、Q两点之间，∴P、Q在双曲线的左支上，且y₁y₂＜0.

又双曲线的渐近线为y=±x,∴k＜-或k＞,即|k|＞,联立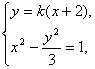

消去x，整理得(3-k²)y²-12ky+9k²=0.y₁y₂=,y₁+y₂=,

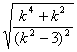∴|y₁-y₂|==6=6≥6

∴S_△PQM=|y₁-y₂|×|FM|=|y₁-y₂|≥9.

综上可知：△PQM面积的最小值是9.