Question

要用总长为20m的铁栏杆，一面靠墙，围成一个矩形的花圃，怎样围法才能使围成的花圃的面积最大？

Answer 1

【答案】分析：设矩形靠墙一面的长为xm，则两端的长为（20-x）÷2m，根据矩形面积公式求面积表达式，再根据性质求最值．
解答：解：设矩形靠墙的一面长为xm，面积为sm²
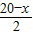
根据题意得s=x×=-x²+10x=-（x-10）²+50
∵-＜0
∴函数有最大值
当x=10时，s最大．
此时矩形两端长为5m．所以当两端各长5m，与墙平行的一边长10m时围成的花圃的面积最大．
点评：本题主要考查函数的最值及其几何意义、函数模型的选择与应用．此题关键在得出面积的表达式，将实际问题转化为函数问题解答，渗透了数学建模的思想．