
【题目】如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
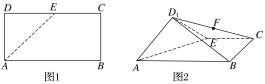
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)线段AB上存在满足题意的点M,且![]() =
=![]()
【解析】
(1)先计算得BE⊥AE,再根据面面垂直性质定理得结果,(2)先分析确定点M位置,再取D1E的中点L,根据平几知识得AMFL为平行四边形,最后根据线面平行判定定理得结果.
(1)证明连接BE,

∵ABCD为矩形且AD=DE=EC=BC=2,
∴∠AEB=90°,即BE⊥AE,
又平面D1AE⊥平面ABCE,
平面D1AE∩平面ABCE=AE,BE平面ABCE,
∴BE⊥平面D1AE.
(2)解AM=![]() AB,取D1E的中点L,连接AL,FL,
AB,取D1E的中点L,连接AL,FL,
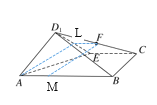
∵FL∥EC,EC∥AB,∴FL∥AB且FL=![]() AB,
AB,
∴FL∥AM,FL=AM
∴AMFL为平行四边形,∴MF∥AL,
因为MF不在平面AD1E上, AL平面AD1E,所以MF∥平面AD1E.
故线段AB上存在满足题意的点M,且![]() =
=![]() .
.


科目:高中数学 来源: 题型:
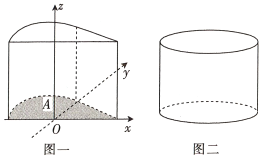
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的![]() 平面内,若函数
平面内,若函数![]() 的图象与
的图象与![]() 轴围成一个封闭的区域
轴围成一个封闭的区域![]() ,将区域
,将区域![]() 沿
沿![]() 轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域
轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域![]() 的面积相等,则此圆柱的体积为__________.
的面积相等,则此圆柱的体积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 实数,函数
实数,函数![]() ,函数
,函数![]() .
.
(Ⅰ)令![]() ,当
,当![]() 时,试讨论函数
时,试讨论函数![]() 在其定义域内的单调性;
在其定义域内的单调性;
(Ⅱ)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥底面ABCD,PD=DC=2,E,F,G分别是AB,PB,CD的中点.
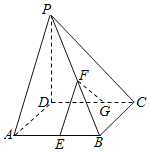
(1)求证:AC⊥PB;
(2)求证:GF∥平面PAD;
(3)求点G到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() ,
,![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
C.当![]() ,
,![]() ,
,![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D.在三棱锥中![]() ,
,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,该三棱锥体积最大值为12
,该三棱锥体积最大值为12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 为圆上一点.椭圆
为圆上一点.椭圆![]() 以
以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() .
.
(Ⅰ)当![]() 点坐标为
点坐标为![]() 时,求
时,求![]() 的值及椭圆方程;
的值及椭圆方程;
(Ⅱ)若直线![]() 与(Ⅰ)中所求的椭圆交于
与(Ⅰ)中所求的椭圆交于![]() 、
、![]() 不同的两点,且点
不同的两点,且点![]() ,
,![]() ,求直线
,求直线![]() 在
在![]() 轴上截距
轴上截距![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P为椭圆C:![]() 1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2
1(a>b>0)上一点,F1,F2分别是椭圆C的左、右两个焦点,|PF1|=2|PF2|,且cos∠F1PF2![]() ,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
,过点F2且斜率为k的直线l与椭圆C交于A,B两点.
(1)求椭圆C的离心率;
(2)若点M(1,![]() )在C上,求△MAB面积的最大值.
)在C上,求△MAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com